Uma amostra de gás ideal se expande de uma pressão e volume iniciais de e para um volume final de .A temperatura inicial é . Se o gás for monoatômico e a expansão for isotérmica, quais são:

A pressão final,

A temperatura final, ?

O trabalho realizado pelo gás?

Refaça os itens anteriores para o caso em que a transformação é adiabática e o gás é monoatômico, e para o caso em que a transformação é adiabática e o gás é diatômico.

Dados:

-Constante dos Gases:

-Pressão atmosférica:

-Gás monoatômico:

Vamos resolver os itens da questão para o caso 1 primeiro:

Temos que achar a pressão final. Lembrando que a transformação é isotérmica, ou seja, a temperatura final é igual a inicial, nossos dados são esses:

Vamos substituir esses dados na equação:

Vamos simplificar logo uma coisa: as temperaturas antes e depois são iguais, então podemos cortá-las da equação:

Queremos saber a temperatura final... Mas lembra que a transformação é isotérmica? Logo, a temperatura final é igual à inicial e vale:

Agora precisamos saber o trabalho que o gás realizou nessa transformação. A equação que usamos é a integral:

Mas como calcular isso se a pressão e o volume variam constantemente numa transformação isotérmica? Segue o gráfico dessa transformação:

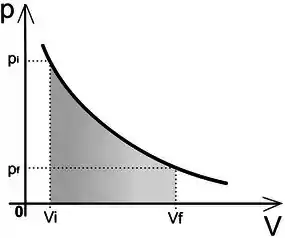
Bom, mas sabemos que a temperatura não varia! Vamos modificar essa integral para alguma que saibamos calcular. Usando a equação geral dos gases para isolar a pressão:

Substituindo na integral:

Notou o pulo do gato no final? Isso porque

Ótimo, pois temos o volume inicial e final. Substituindo na equação os valores e , , e convertendo as unidades:

Ufa! Vamos agora aos outros casos.

-Caso2:

Como agora estamos lidando com uma transformação adiabática, vamos usar:

Com:

Além disso, temos os mesmos valores iniciais para o estado que o passo anterior. Logo, aplicando os valores de pressão e volume que temos na equação, podemos encontrar a :

Eita, agora não podemos dizer que , pois a transformação não é isotérmica! Então a gente vai ter que apelar pro Piviti-Povóto:

Bom, precisamos calcular o trabalho realizado por um gás numa transformação adiabática! Como o gás é monoatômico, usaremos:

é fácil de ser obtido pois sabemos e :

E o pode ser obtido usando a equação geral dos gases e as condições iniciais(convertendo as unidades de pressão e volume):

Substituindo as duas quantidades na fórmula:

(:

-Caso3:

O caso 3 é bem similar ao caso 2. A única diferença é que o gás é diatômico. Sim, essa questão é um pouco repetitiva (u.u), mas ela nos ajuda a compreender as diferenças de cada transformação!

Vamos resolver o caso 3 mais rapidamente, lembrando-se de utilizar as mesmas condições de temperatura, volume e pressão iniciais que usamos nos outros:

Vamos usar, novamente, a equação:

Precisamos só recalcular o valor de para um gás diatômico:

Aplicando esse e os outros valores na equação:

Vamos usar de novo Piviti-Povotó pra achar a temperatura final:

Novamente, como a transformação é adiabática, podemos escrever:

Só que os gases diatômicos têm 5 graus de liberdade, como vimos na teoria, então:

O é fácil de calcular já que temos e :

E o pode ser obtido usando a equação geral dos gases e as condições iniciais (convertendo as unidades de pressão e volume):

Logo, substituindo na equação do trabalho: