​A figura a seguir mostra, em escala, o diagrama que descreve dois processos, e , que uma certa amostra de gás ideal pode sofrer a partir do mesmo estado inicial . O processo leva o gás para o estado final , enquanto o processo o leva ao estado final . Os estados 2 e 3 apresentam a mesma temperatura.

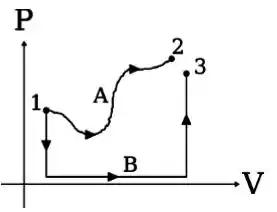
Considere: A variação de energia interna do gás, , o calor recebido pelo gás, , e o trabalho realizado sobre o gás, . A comparação correta dos valores dessas grandezas (dos valores com o sinal, não dos módulos dos valores!) nos dois caminhos é

Para a variação de energia:

Para o trabalho realizado sobre o gás

Para o calor recebido pelo gás

Agora, vamos analisar a variação de energia interna. Como a variação de energia interna não depende do caminho adotado, apenas dos estados iniciais e finais.

Precisamos apenas saber em qual estado a temperatura é maior, pois como eles saem do mesmo estado inicial, onde houver a maior variação de temperatura, significa que tivemos a maior variação de energia interna.

Como a variação da energia interna depende de qual tipo de molécula, número de mols e da variação de temperatura. E a única coisa que muda de um processo para o outro é a temperatura final.

Então, onde tiver a maior temperatura, terá a maior variação de energia interna.

Bem, vamos lá descobrir a temperatura final, né?

Opaaa! O enunciado já disse que elas são iguais, então a variação de temperatura é a mesma, logo a variação de energia interna é igual,

Assim a resposta do item é a alternativa .

Agora só falta descobrirmos a relação entree , pela primeira lei da termodinâmica temos que

Como

Podemos escrever

Para facilitar, podemos isolar trabalho de um lado e calor de outro

Como, vimos que

Então

Boa!! Então, concluímos que

A reposta da é a a alternativa

Agora, olha que sacanagem as respostas!