PUCRIO – Física 2 – 2020.1 – G3 – M. Escolha
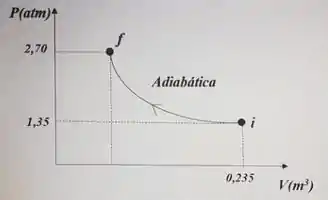
. Um gás ideal , sofre um processo termodinâmico de compressão descrito pela figura abaixo. A pressão e o volume inicial são e . A pressão final é . Qual é o trabalho realizado pelo gás?
.
.
.
. Nenhuma das alternativas
.
.
.
.
Passo 1
Vem comigo resolver essa questão!
Temos em mãos um processo termodinâmico adiabático. Então sobre esse processo sabemos que:
E como temos um gás ideal e diatômico temos que:
Então para achar o trabalho podemos usar o seguinte:
Onde , temos:
Mas não sabemos o valor das temperaturas, mas temos como achar o fator da equação dos gases ideais, da seguinte maneira:
Mas para isso precisamos saber o volume final já que o enunciado não nos dá, para isso vamos usar o seguinte:
Mãos à obra então!
Passo 2
Vamos primeiro achar o volume final , temos:
Substituindo os valores que temos, ficamos com:
Passo 3
Agora vamos para a próxima etapa que é calcular o valor de para o estado inicial e para o estado final do processo.
Começando com o inicial, temos:
Vamos usar que e para isso precisamos usar a pressão em , onde:
Assim, temos que:
Voltando para a fórmula anterior temos:
Logo temos:
Passo 4
Agora vamos calcular o produto para o estado final, temos:
Temos que passar a pressão de para , assim:
Então temos o seguinte:
Assim temos que:
Passo 5
Agora vamos encontrar o trabalho, temos:
Substituindo o que sabemos, temos:
Assim temos que:
Então não temos nenhuma alternativa que bata com o valor que encontramos, assim a alternativa correta é a letra .
Resposta
. Nenhuma das alternativas