Uma quantidade de ar (considerado um gás ideal diatômico, cujo calor especifico molar a volume constante vale ou é primeiro resfriada sem variação de volume, e depois expandida sem variação de pressão, como mostra o caminho , na figura abaixo.
Compare a temperatura final do gás com a sua temperatura inicial
Quanto calor o ar recebe do seu meio ambiente durante o processo ? Explique.
Se, em vez disso, o ar se expandisse do estado ao estado pelo caminho mostrado em linha reta, quanto calor ele receberia do seu meio ambiente?
Pelo novo caminho, qual a variação da energia interna ao sair do estado ao ? E pelo caminho original? Explique.
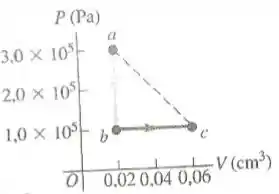
Passo 1
Temos que comparar a temperatura do estado inicial com a temperatura final, estado .
Como temos a pressão e volume dos dois estados (encontramos pelo gráfico) e o gás não muda, isso significa que o número de mols não varia e por isso podemos usar “PiViTi-PoVoTo”
O sistema internacional de medida pede que o volume seja dado em metros cúbicos e a pressão em . A pressão dada pelo gráfico está ok. Mas o volume não, então mudaremos. E por isso multiplicaremos o volume dado pelo gráfico por . Pois é igual a .
Então substituindo os valores de pressão e volume temos:
Para essa equação ser respeitada então .
Então a temperatura inicial e final são iguais.
Passo 2
Queremos saber a quantidade de calor transferida no processo. Para isso vamos usar a primeira lei da termodinâmica.
Como o estado e tem a mesma temperatura. Então a variação da energia cinética é zero. Então a transferência de calor é igual ao trabalho realizado.
Tendo um diagrama calcular o trabalho é moleza. Então vamos descobrir a quantidade de calor calculando o trabalho no processo .
Por que é moleza calcular o trabalho tendo o diagrama , porque o trabalho é igual a área abaixo da curva que descreve o processo .
Então a quantidade de calor recebida pelo gás no processo é de .
Passo 3
Agora o caminho mudou, mas o estado inicial e final continuam e como a variação da energia interna depende apenas do estado inicial e final, então continua sendo zero a variação de energia interna e por isso a quantidade de calor é igual ao trabalho.
Assim como no item , vamos calcular o trabalho pela área do gráfico.
Como o caminho mudou a curva é outra e por isso teremos outra área.
A área do caminho forma um trapézio de base maior , base menor e altura .
Assim o trabalho será:
Então a quantidade de calor recebida pelo gás no processo ac é de .
Passo 4
Já respondemos esse item para fazer os itens anteriores. Como a variação da energia interna é uma função de estado, ou seja, só depende do estado inicial final e este não muda, continua sendo e .
Então a variação da energia interna no processo é igual a do processo .
E como a temperatura no estado inicial e final é a mesma. Então a variação da energia interna é zero.
Resposta