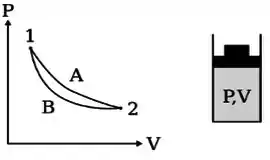
Um gás ideal está confinado em um cilindro com pistão que pode se mover sem atrito. O gás pode sofrer as transformações ou do estado para o estado .
É correto afirmar que:
Passo 1
Vamos começar analisando o trabalho de cada processo, como vimos na teoria o trabalho EXERCIDO pelo gás é a área sob a curva no gráfico , positivo se a curva é no sentido hórario.
Visto isso, como a curva , está acima da curva , então
Porém a questão deseja o trabalho sobre o gás, este terá o mesmo módulo, porém sinal oposto (negativo), por isso:
Passo 2
Como os dois caminhos vão do estado para o estado , temos que o ponto inicial e final é o mesmo, sendo assim a variação de energia interna é a mesma, pois variação de energia interna é uma função de estado.
Pela primeira lei da termodinâmica, podemos reescrever essa igualdade como
Colocando trabalho par um lado e calor para outro, temos
Como, vimos que
Então
Resposta
Alternativa