Três amostras idênticas de um mesmo gás ideal estão confinadas em um cilindro fechado por um êmbolo móvel. A força que o êmbolo exerce sobre o gás é ajustada para que o gás esteja confinado com a pressão inicial e com o volume inicial do interior do cilindro
O gás da amostra é aquecido, e o volume da câmera é alterado, mantendo-se o valor da força inalterado.
O gás da amostra é aquecido mantendo-se a posição do êmbolo inalterada.
O êmbolo comprime o gás da amostra suficientemente rápido para que o calor trocado entre gás e vizinhança seja desprezível.
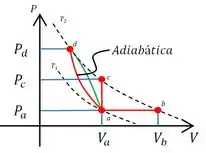
Todos os processos terminam à mesma temperatura e estão ilustrado no mesmo diagrama a seguir.
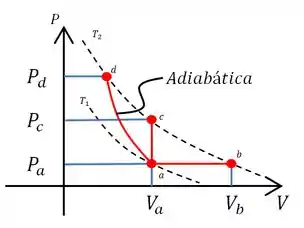
Qual a transformação, ou que descreve cada situação e ?
Ordene os processos e em ordem crescente de trabalho realizado pelo gás.
Ordene os processos e em ordem crescente de calor recebido do ambiente. Justifique.
As variações da energia interna são diferentes? Justifique.
Indique na figura um processo possível em que a variação da energia térmica seja a mesma que para o processo e na qual o gás ceda calor para o ambiente em vez de receber.
Passo 1
Para descobrirmos qual a transformação de cada situação temos que prestar atenção na descrição de cada processo. Vamos a primeira situação
Situação – O gás é aquecido, o volume se altera, mas a força é mantida a mesma. O enunciado acima diz que a força é a responsável por gerar a pressão , como a força não se altera então a pressão continua a mesma.
Assim, esse processo é isobárico e no diagrama o processo que mantem a pressão é o “ab”.
Situação O gás é aquecido e a posição do embolo é mantida, ou seja, o volume não se altera. Então esse processo é isovolumétrico e o processo no diagrama que mantem o volume é o .
Situação O gás é comprimido tão rápido que a troca de calor é desprezível. Se a troca de calor pode ser considerada zero. Então é um processo adiabático, pois não ocorre troca de calor. A própria figura indica qual processo é adiabático e por isso esse processo é o que representa a situação .
Passo 2
O trabalho de um gás é igual a área sobe a curva que descreve o processo no diagrama . Então para ordenar os processos de acordo com o trabalho basta vermos qual tem maior área sob o gráfico.
O processo não tem área, pois é uma linha vertical e por isso o trabalho é zero.
O processo tem uma área , como a variação de volume é positiva o trabalho será positivo.
No entanto no processo “ad” a variação do volume é negativa então o trabalho será negativo.
Então a ordem dos trabalhos será:
Passo 3
O enunciado diz que todos os estados finais tem a mesma temperatura . E como todos saíram do mesmo ponto com a temperatura então a variação da energia interna será a mesma em todos os processos.
Pois a variação da energia interna depende apenas da variação da temperatura e do número de mols e tipo do gás. Como tudo se mantém inalterado não importando o processo, então
E pela primeira lei da termodinâmica temos que:
Por esta equação podemos ver que se o trabalho em é maior que o trabalho em , então q quantidade de calor em deve também ser maior que para manter a igualdade.
Isso também vale para o processo .
Então a relação entre a quantidade de calor é igual a de trabalho.
Passo 4
Para justificar o nosso raciocínio no item respondemos esse item. Lá vimos que a temperatura nos estados e são a mesma e por isso a variação da energia interna será a mesma.
Passo 5
Bem, queremos um processo em que a variação da energia interna seja a mesma e a quantidade de calor seja negativa. Para a variação energia interna se a mesma, basta que os estados escolhidos estejam em cima na isoterma em que e ficam.
O problema é garantir que a quantidade de calor seja negativa. Para isso vamos analisar o processo .
No processo “ac” a troca de calor é zero, , então pela primeira lei:
Como o trabalho é negativo, qualquer processo entre os pontos que tenha trabalho menor que o trabalho no processo a transferência de calor será negativa. Porque:
Então, se , será negativa.
E quando é negativo significa que o gás está cedendo calor.
Agora vamos criar um processo em que o trabalho seja menor que .
Sabemos que o módulo do trabalho é igual a área sobre a curva e o sinal será dado pela variação do volume. Como a variação do volume entre e é negativa. Basta fazermos um caminho em que a área sob a curva seja maior que área sobe a curva . Existem varias opções, uma opção é a da curva em verde:
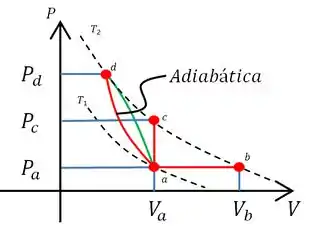
Resposta
Situação – Processo ; Situação – Processo ; Situação – Processo