Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Primeira Lei da Termodinâmica em Gases

Ver Teoria
Exercício 751234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374767778798081828384858687888990919293949596979899100

Enunciado

Primeira Lei e Gases Ideais

Um gás de moléculas de nitrogênio ( N 2 ) ocupa um volume V i = 1,0 × 10 3   c m 3 à temperatura de T i = 600   K . Sabe-se que existem 12,0 × 10 20   m o l é c u l a s / c m 3 no volume ocupado pelo gás. Considere o gás ideal (dado: 1   m o l de N 2 tem massa igual a 28   g ).

  1. Determine o número n de mols da amostra.
  2. Determine a energia cinética média (translação + rotação) por molécula do gás.
  3. Determine, a partir da energia cinética média de translação, a velocidade quadrática média das moléculas do gás.

    4. O gás, nas mesmas condições iniciais acima, é agora submetido a uma expansão em que a pressão aumenta linearmente com o volume. A pressão e o volume no estado final são duas vezes maiores que no inicial ( V f = 2 V i e p f = 2 p i ).

  4. Esboce o diagrama p × V do processo termodinâmico e obtenha, em função de n , R e T i , o trabalho realizado pelo gás e o calor fornecido ao gás nesse processo.

Dados:

N A = 6,0 × 10 23 m o l - 1

k = 1,38 × 10 - 23   J / K

Passo 1

Temos uma informação do enunciado: Existem: 12,0 × 10 20   m o l é c u l a s / c m 3 .

Vamos calcular, então, o número de moléculas do gás usando o volume ocupado pelo mesmo, certo?

N = 12,0 × 10 20 . 1,0 × 10 3 = 12,0 × 10 23 m o l é c u l a s

Agora vamos calcular o número de mols usando a constante de Avogadro:

n = N N A = 12,0 × 10 23 6,0 × 10 23 = 2 m o l

Passo 2

b):

A energia cinética média de um gás é dada pela fórmula:

E c = g 2 k T

Onde g é o número de graus de liberdade do gás. Sendo a molécula diatômica, a mesma tem dois graus de liberdade de rotação e três graus de liberdade de translação. Logo:

g = 5

E c = 5 2 1,38 × 10 - 23   . 600 = 2,07 × 10 - 20 J

Passo 3

c):

Podemos comparar a equação que usamos agora há pouco com a outra abaixo:

3 2 k T = E c i n t r a n s l a ç ã o = m v q 2 2

Onde m é a massa de uma molécula e v q é a velocidade quadrática média do gás, o que queremos saber.

Usamos ali os três graus de liberdade, apenas, pois devemos fazer as comparações apenas com a energia de translação, excluindo a de rotação. Logo:

E c i n t r a n s l a ç ã o = 3 ( 1,38 × 10 - 23 ) ( 600 ) 2 = 1,24 × 10 - 20 J

Então,

Vamos calcular primeiro m :

O enunciado nos diz que a massa de um mol é 28 g = 28 × 10 - 3 k g . Bom, sabemos quantas moléculas tem em um mol, então basta a gente dividir o valor de massa pelo número de moléculas de um mol:

m = 28 × 10 - 3 6 × 10 23 ≅ 4,7 × 10 - 26 k g

Como já calculamos a energia cinética média no item anterior, temos que:

2 E c i n t r a n s l a ç ã o m = v q 2 = 2 . 1,24 × 10 - 20 J 4,7 × 10 - 26 ≅ 0,52 × 10 6

∴

v q = 0,52 × 10 6 ≅ 729 m / s

Passo 4

d):

O gráfico dessa transformação é:

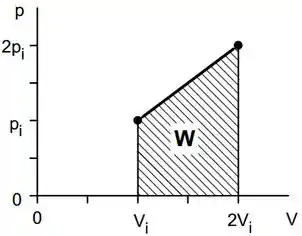
A área sombreada corresponde ao trabalho realizado pelo gás. Podemos calcular o trabalho realizado pelo gás, então, calculando a área acima:

A = B + b h 2

Sendo h = 2 V i - V i = V i

B = 2 p i

b = p i

Logo:

W = A = 3 p i V i 2 = 3 2 p i V i

Vamos usar a equação geral dos gases:

p V = n R T

Logo:

W = 3 2 p i V i = 3 2 n R T i

Podemos calcular a variação de energia interna através da fórmula:

∆ U = n c v ∆ T = n c v T f - T i

Precisamos descobrir a T f . Como o gás pe diatômico, temos que:

c v = 5 2 R

Vamos usar a relação:

p i V i T i = p f V f T f

Sendo p f = 2 p i e V f = 2 V i :

p i V i T i = 4 p i V i T f   → T f = 4 T i

Então a variação de energia interna será:

∆ U = n . 5 2 R . 4 T i - T i = 15 n R T i 2

Bom, e nós queremos descobrir o calor, certo? Então, aplicando a primeira lei:

∆ U = Q - W → ∆ U + W = Q = 3 2 n R T i + 15 n R T i 2 = 18 n R T i 2 = 9 n R T i

Resposta

a):

n = 2 m o l

b):

2,07 x 10 - 20 J

c):

729 m / s

d):

Q = 9 n R T i

Exercícios de Livros Relacionados

Calcule o trabalho realizado por um agente externo durante uma compressão isotérmica de 1,00m o l de oxigênio de um volume de 22,4L a 0 ° C e 1,00a t m para um volume de 16,8L .
Uma amostra de um gás ideal sofre uma expansão de uma pressão e volume iniciais de 32a t m e 1,0L para um volume final de 4,0L . A temperatura inicial é 300K . Se o gás é monoatômico e a expansão é is
O calor Q flui para dentro do gás monoatômico ideal, e o volume aumenta enquanto a pressão é mantida constante. Que fração da energia calorífica é usada para realizar trabalho de expansão do gás?
Considere a seguinte série de processos quase-estáticos pelos quais um sistema passa sequencialmente: (1) uma expansão adiabática, (2) uma expansão isotérmica, (3) uma compressão adiabática e (4) uma
Um gás ideal sofre um processo durante o qual P V = c o n s t a n t e e o volume do gás diminui. A temperatura aumenta, diminui ou permanece a mesma durante este processo? Explique.