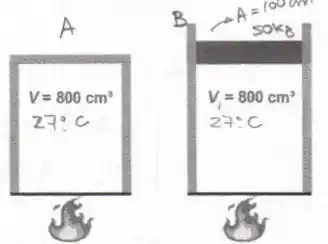
Dois recipientes contêm quantidades idênticas de um gás monoatômico a e de volume inicial , cada. O recipiente é rígido. O recipiente dispõe de um pistão, com área de e massa de , que pode deslizar sem atrito para cima ou para baixo. Os recipientes são colocados sobre queimadores idênticos e aquecidos durante o mesmo intervalo de tempo.
- A temperatura final do gás contido em será maior do que, menor do que ou igual a temperatura do gás em ? Explique.
- Represente os dois processos num mesmo diagrama
- Quais são as pressões inicias nos recipientes e
- Suponha que os aquecedores forneçam de potência e que fiquem ligados durante Qual é o volume final do gás no recipiente
Constantes:
Passo 1
a)
Vamos usar a primeira lei da termo pra resolver isso:
O cilindro é rígido, ou seja, o aquecimento não levará a uma realização de trabalho. Assim:
Já o cilindro possui um pistão, logo, haverá a realização de trabalho:
Como:
Podemos chegar a conclusão de que:
Como a energia interna é uma função da temperatura, podemos dizer que a variação da temperatura em também será menor que em
Ou seja, a temperatura final do gás em será maior que o gás de
Passo 2
b)
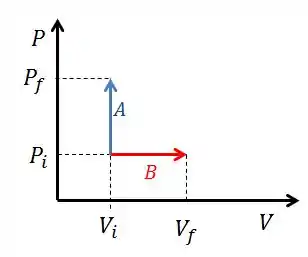
Passo 3
c)
Nós não sabemos o número de mols nos recipientes, então não podemos usar a equação dos gases ideais.
Porém, sabemos que no recipiente , que tem um pistão de massa , existe o equilíbrio de forças e pressões.
Assim:
A pressão devido o peso do pistão pode ser calculada por:
Assim:
Assim, a pressão inicial no recipiente e ( elas são iguais):
Passo 4
d)
sofre uma expansão isobárica( a pressão constante):
Assim:
O calor pode ser obtido através da potência e da variação de tempo:
Tendo o calor, basta a gente descobrir a variação de energia interna, pois ai descobriremos , por fim, o trabalho.
porque acontece à pressão constante. Como o gás é monoatômico:
Não sabemos , porém podemos descobrir, já que já sabemos todas as informações do estado inicial:
Podemos descobrir a temperatura final através da relação:
Assim:
Voltando à equação inicial:
Sendo:
Assim:
Assim, o volume final será:
Resposta
a)
a temperatura final do gás em será maior que o gás de
b)
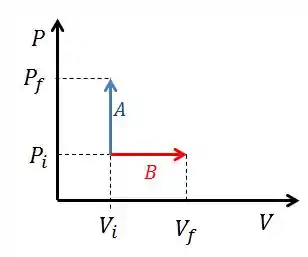
c)
d)