A figura abaixo mostra três possíveis expansões de um gás ideal monoatômico, que encontra-se inicialmente no estado (cujo volume é ) para os estados finais , ou , todos de volume , através de três processos reversíveis diferentes: -Transformação isobárica; -Transformação isotérmica e -Transformação adiabática.
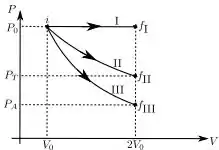
Sobre tais processos é INCORRETO afirmar que:
(a) A maior variação do módulo da energia interna do gás ocorre no processo adiabático.
(b) No processo isotérmico todo trabalho é transformado em calor.
(c) O trabalho realizado pelo gás é menor no processo adiabático.
(d) A maior troca de calor se dá no processo isobárico.
(e) As temperaturas finais terão a relação .
Passo 1
Então, aqui foi dado um gráfico com 3 processos de expansão de um gás ideal monoatômico e nos pede o item incorreto. Vamos analisar item por item!
Passo 2
Na letra (a) temos uma comparação das variações de energia interna ) nos 3 processos.
Vamos só relembrar que no processo isobárico para um gás monoatômico:
Como o número de mols é igual em todos os 3 processos, repare que a única coisa que pode variar nessa expressão é o . E quanto maior essa variação, maior será .
Então, bora analisar isso aí!!
Passo 3
O primeiro processo se trata de uma expansão isobárica, ou seja, sem variação na pressão.
Então, temos que:
Sendo , e vamos ficar com:
E fazendo umas continhas, vamos encontrar:
Dessa forma, no primeiro processo,
Passo 4
No segundo processo, temos uma expansão isotérmica. Então:
e
Passo 5
No terceiro processo, uma expansão adiabática, podemos usar a relação:
Onde, e :
Fazendo mais algumas continhas:
Então:
Passo 6
Agora só falta comparar os valores de que achamos para cada processo e vamos encontrar:
Então:
Logo, a letra (a) tá incorreta 😊 e ela é nossa primeira resposta!
Primeira?! Não era uma incorreta? Pois é, mas nessa questão rolou um probleminha de português rs e foram consideradas duas respostas! Sem problemas!! Estamos preparados para tudo! Heheh
Passo 7
Vamos analisar essa letra (b), agora.
O fato de ser uma transformação isotérmica nos diz que , como vimos no passo 4, e, pela primeira lei, .
Então, até aí, ok! Só que olha o que a (b) nos diz:
No processo isotérmico todo trabalho é transformado em calor.
Só que numa expansão é o calor que se converte em trabalho e não o contrário!!
Logo, a alternativa (b) também está errada!
Ufa, agora sim acabamos essa questão.
Resposta
Alternativas (a) e (b) estão incorretas.