Um mol de um gás monoatômico ideal é submetido a um ciclo completo ABCA em três etapas (veja o diagrama p-V na figura abaixo):
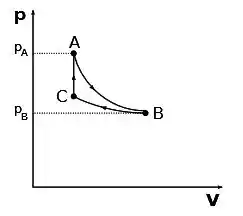
Etapa A → B: Expansão adiabática, onde .
Etapa B → C: Contração isotérmica a .
Etapa C → A: Aumento de pressão a volume constante.
Determine o trabalho e o calor total transferido no ciclo. Se necessário use e .
Passo 1
Em um ciclo termodinâmico a primeira lei dos gases, nos garante que:
Sendo que no ciclo
Então descobrindo um, descobriremos os outros facilmente.
Vamos calcular o trabalho de cada etapa
Na etapa AB,
A temperatura nós sabemos e é , pela relação:
Como para um gás monoatômico
Temos que
Assim
Agora podemos calcular o trabalho
Passo 2
O Trabalho do processo é dado por
Observe que
O enunciado deu que no processo adiabático
, bem sabendo disso e sabendo que
Temos que
Assim,
Passo 3
Por fim o trabalho do processo , como nele
Passo 4
Por fim, o trabalho final é
Sendo