Considere um cilindro contendo um mol de gás monoatômico tampado por um êmbolo imerso em uma mistura de água e gelo (ver figura). O êmbolo é rapidamente empurrado para baixo até a posição 2 através de um processo adiabático, reduzindo o volume do gás a um terço do volume inicial. É mantido nessa posição até que o gás volte ao equilíbrio térmico com a mistura de gelo e água. Em seguida o êmbolo é levantado até a posição inicial através de uma transformação isotérmica (ver diagrama da figura). Calcule:
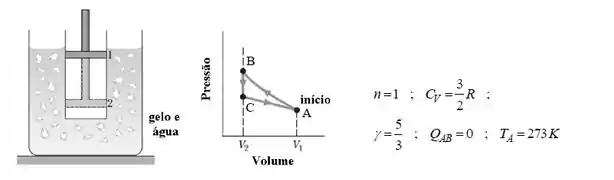
- a temperatura do gás assim que o êmbolo chegar à posição 2;
- quanto gelo derrete no processo até o gás voltar ao equilíbrio térmico, com o êmbolo na posição 2;
- o trabalho feito pelo gás na expansão isotérmica;
- a quantidade total de gelo que foi derretida no processo inteiro;
- a variação de entropia do sistema gás-água-gelo.
Passo 1
Bom galera, quando estamos falando de um processo adiabático, ou seja, aquele em que não há variação de calor, correspondente a posição do diagrama, vale a equação:
Onde é definido da seguinte forma: ,
Passo 2
Para calcularmos a quantidade de gelo que foi derretido, temos que saber primeiro o quanto de calor foi cedido/recebido, vocês têm ideia de como faremos isso?

Se sua resposta foi: Utilizar a formula , você acertou!
Então vamos lá. O cálculo da quantidade de calor perdido no trecho , se dá por:
Calculado a quantidade de calor que foi recebido pelo gelo, agora podemos ver a quantidade de gelo que foi derretido:
Onde é o calor latente de fusão do gelo (a 0°C),
Passo 3
Sabemos lá da teoria da primeira lei da termodinâmica em gases que a numa expansão isotérmica temos , ou seja, , e que o trabalho nesse processo pode ser calculado como:
Passo 4
Nós sabemos que a variação da energia interna é uma função de estado que só depende do estado inicial e final, não é?!

Em um ciclo esses valores são iguais! Logo:
Portanto, para sabermos a quantidade de calor total recebida pelo gelo, basta somarmos:
O que nos dá:
Passo 5
A entropia assim como a energia interna é uma função de estado, lembra? Portanto num ciclo a .
Mas além do ciclo termodinâmico, é possível que calculemos a entropia associada a fonte quente/fria do sistema, no nosso caso está quando o gelo recebe calor da fonte. Para isso calculamos da seguinte maneira: