O diagrama abaixo descreve processos diferentes entre dois estados inicial e final, respectivamente e , sofridos por 1 mol de um gás ideal. Considere como sendo .
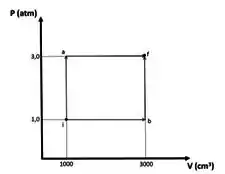
Considerando os dois trajetos indicados no diagrama p-V para se levar o sistema do estado para o estado , a saber e , sabe-se que o calor a ser fornecido ao sistema no trecho é de , no trecho é de e no trecho é de . Qual é então o calor que deve ser fornecido ao sistema no trecho ?
.
.
.
.
.
.
O processo ia tem que ser um processo adiabático, ou seja, sem trocas de calor.
Passo 1
Em um processo termodinâmico ele sempre respeita a primeira lei da termodinâmica que diz que:
E como a energia interna é uma função de estado, ou seja, não depende do caminho que percorreu apenas do estado inicial e final então, para ambos os caminho a energia interna será .
Então podemos dizer que:
Os trabalhos de cada caminho é fácil descobrir, pois temos o gráfico e o trabalho é igual a área abaixo do curva no gráfico .
Então o trabalho do trajeto é
E o trabalho do trajeto é
E o calor transferido no trajeto é dado pela soma dos calores de com
Beleza, vamos substituir esses valores na equação que temos
Passo 2
Agora que sabemos a quantidade de calor transferida de , podemos descobrir quanto foi transferido de , pois o calor total transferido é a soma do calor transferido em cada trecho. E o enunciado nos forneceu quanto foi transferido de .
Resposta
Alternativa