Um recipiente cilíndrico, que tem área de base e altura quando a temperatura é de , é feito de vidro (pyrex) com coeficiente de dilatação linear. O recipiente está inicialmente a uma temperatura e contém um único bloco de gelo que ocupa todo seu volume. O sistema recipiente – bloco de gelo está em equilíbrio térmico.
PARTE I
a) Determine o calor total que é necessário ceder ao sistema para derreter todo o gelo e obter água no estado líquido à mesma temperatura .
b) Determine a altura h da água à temperatura , no recipiente, uma vez completada a transição de fase.
PARTE II - Considere agora que o sistema (recipiente de pirex e água) se encontre na temperatura e com água (coeficiente de dilatação volumétrico ) no estado líquido até uma altura .
c) Determine uma expressão literal em função dos dados do problema para a altura máxima inicial da água no recipiente de modo que não seja derramada água quando o sistema alcançar temperatura.
d) Determine a razão entre || o calor cedido para a água e || o calor cedido ao recipiente para levar o sistema do item (c) da temperatura inicial até a temperatura final . A massa do recipiente de pyrex é .
Dado da questão:
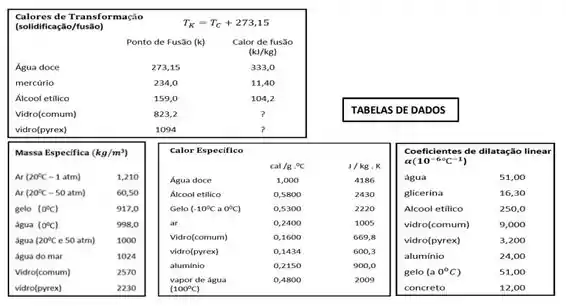
Passo 1
a) Para calcular o calor total para derreter o gelo temos que:
Substituindo os valores
Passo 2
b) Uma vez que foi completada a transição de fase, temos que:
Passo 3
c) Bom pessoal, temos a seguinte situação: Não queremos que a água entorne quando ela atingir a , para isso:
Passo 4
d) Vamos descobrir qual a altura máxima da água no recipiente quando temos uma .
Agora, podemos calcular a quantidade de calor absorvido pela água ao atingir essa temperatura:
E a quantidade de calor absorvida pelo recipiente pra atingir essa temperatura:
Logo, a razão entre || o calor cedido para a água e || o calor cedido ao recipiente é
Resposta
a)
b)
c)
d)