Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 19 – Problemas - 45.
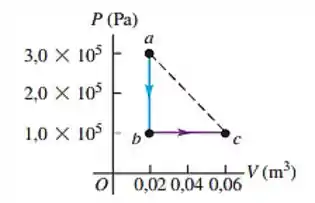
(Cap 19 – Prob 45) Um volume de ar (considerado um gás ideal) é primeiro resfriado sem variação de volume, e depois expandido sem variação de pressão, como mostra o caminho na Figura 19.30. a) Compare a temperatura final do gás com a sua temperatura inicial. b) Quanto calor o ar troca com seu meio ambiente durante o processo ? O ar absorve calor ou libera calor durante esse processo? Explique. c) Se, em vez disso, o ar se expandisse do estado ao estado pelo caminho mostrado em linha reta, quanto calor ele trocaria com seu meio ambiente?
Passo 1
Falai galerinha do Responde ai, bora fazer mais uma?
a) O enunciado diz que o volume de ar é considerado um gás ideal, vamos usar a equação de gases ideias para esse problema:
E considerar os estados final e inicial, igualando os dois casos, a gente fica com:
Separando as temperaturas do resto:
E substituindo os valores de volume e pressão para os dois estados:
Então:
Passo 2
b) Como as temperaturas inicial e final são iguais, isso implica . Além disso, o processo não possui variação de volume, então e todo o trabalho está no processo . Assim:
E como possui pressão constante, podemos usar a equação:
Para calcularmos o trabalho do caminho que será o trabalho de todo o processo:
Repare que convertemos as unidades do volume de centímetros cúbicos que está no gráfico para metros cúbicos por causa das unidades internacionais.
Assim:
Passo 3
c) Já que temos as bases maior e menor e a altura do trapézio composto pelo triangulo mais o retângulo formado entre o eixo do volume e a parte de baixo do triangulo, podemos usar a equação do trapézio para calcularmos o trabalho realizado pelo gás nesse caso:
E como a energia interna do gás não varia, a primeira lei da termodinâmica fica:
Assim o calor será: