UFRJ, Álgebra Linear, P2 -2017.2, Questão 9
Seja uma matriz :
(a) É possível que seja a união de duas retas distintas de e seja um plano de
(b) É possível que seja e seja um subespaço de dimensão 4
(c) É possível que seja uma reta de e seja um plano de
(d) É possível que seja um plano de e seja um plano de
Passo 1
Vamos analisar essa matriz, se ela é o nosso TNI vai ficar assim:
Sendo que a imagem está contida no contradomínio, o e por isso deve ter dimensão menor ou igual a 3!
Vamos agora ver as opções.
Passo 2
(a) É possível que seja a união de duas retas distintas de e seja um plano de
Está opção é incorreta pois o núcleo é um subespaço vetorial do domínio e união de duas retas distintas nunca é um subespaço vetorial por não ser fechado para a soma!
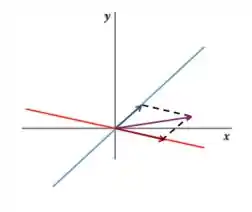
Ou seja, ao somar dois vetores de retas distintas, o resultado pode não pertencer a nenhuma das retas:
(b) É possível que seja e seja um subespaço de dimensão 4
Como vimos no passo 1, a imagem é um subespaço do , logo impossível que ela tenha dimensão 4! E consequentemente, pelo TNI, fica impossível que o núcleo tenha dimensão nula.
(c) É possível que seja uma reta de e seja um plano de
Nesse caso, não bateria com o teorema núcleo imagem:
(d) É possível que seja um plano de e seja um plano de
Essa está correta! Vamos conferir o TNI:
Resposta
(d)