Achar a equação da reta tangente à curva
No ponto
Passo 1
Antes da gente partir pras contas, vamos entender direitinho o que a questão quer: uma equação de reta tangente. Beleza, se a gente vai ter que modelar, vamos ver como a equação genérica funciona:
Agora vamos ver o que é o que aí. Primeiro, essa equação vale pro ponto de tangência específico . Como esse ponto é dado na questão, e é , já dá pra compeltar alguma coisa:
Ok, mas e esse aí? Bem, ele vai ser a inclinação da reta tangente! E quem é a inclinação se não o valor da primeira derivada da curva no ponto de tangência? Vamos ter então que:
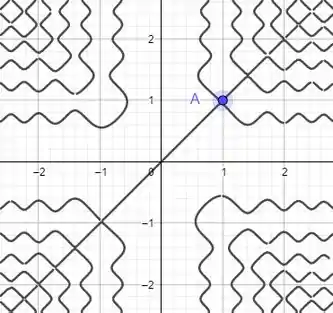
Mas calma, tem algo estranho aí. Olha bem pra curva:
Seja
Como poderemos escrever explicitamente o como função de pra derivar? Bem, nem sempre dá. Quando não dá, a gente deriva implicitamente mesmo, ok?
Passo 2
Vamos derivar agora implicitamente a equação da curva. Derivando dos dois lados:
Usando a regra do produto, a derivada fica:
Como a derivada é em relação à , usando a regra da cadeia, temos então que
E é agora que o resultado do ponto de tangência volta, porque se aplicarmos de novo, vamos ter que e . Pra não embolar, vamos substituir primeiro por . Vamos ter:
Agora substituindo , temos:
Por fim, substituímos por , e logo:
A equação da reta tangente vai ser então:
E olha que doida que é essa curva: