Seja a reta tangente à curva dada pela equação
No ponto . Calcule a área do triângulo formado por e os eixos coordenados.
Veja abaixo uma figura ilustrativa:
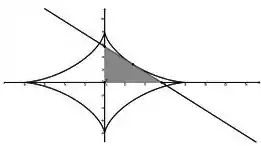
Passo 1
Vamos traçar o plano para resolver essa questão: primeiro encontramos a reta tangente, descobrimos os lados do triângulo (nos interceptos dos eixos), então calculamos sua área.
Como qualquer reta tangente, essa terá coeficiente angular dado pela derivada no ponto tratado. Para derivar a curva aí a gente vê que temos que usar a derivação implícita no termo , depois disso é só substituir direto o ponto tratado:
Substituindo o ponto :
Então, modelando a reta tangente por vemos que seu coeficiente angular valerá . Para descobrir o coeficiente linear basta substituir a equação no ponto trabalhado, :
A reta tangente ao ponto é .
Passo 2
Procuramos agora onde a reta toca cada eixo, o que corresponde a cada um dos lados do triângulo. O coeficiente linear é o valor de no ponto em que a função toca o eixo . Assim, o lado horizontal do triângulo será:
No ponto onde a reta toca o eixo temos . Assim:
Achamos o mesmo valor para os dois lados. Como a área do triângulo é dada pela metade do produto entre a altura e a base, ficamos assim: