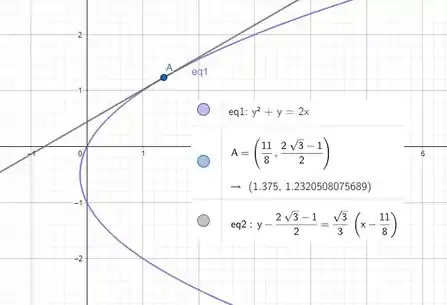
Seja um ponto da curva tal que a reta tangente em faz um ângulo de com o eixo . Quais são as coordenadas de ?
Passo 1
Bora lá achar essas coordenadas. Pra isso, vamos lembrar que a equação de uma reta tangente é dada por:
Onde:
Como temos informações sobre a inclinação da reta tangente, vamos focar no valor de , beleza? Afinal, é exatamente isso que essa letra representa! Como não dá pra derivar explícitamente, vamos derivar implicitamente mesmo (em relação a ):
E logo:
Ok, mas e daí? Como isso ajuda? Bem, pensa comigo, sabemos o ângulo, e sabemos que inclinações de retas são a tangente desse ângulo. Oras! Então temos tudo que precisamos
Juntando os dois resultados:
O que é o mesmo que:
Passo 2
Beleza, achamos a coordenada do ponto de tangência. Falta a . Pra isso, podemos simplesmente pegar a equação da curva e trocar por e por . Saca só como fica:
Por fim:
O ponto de tangência terá as coordenadas:
Passo 3
Esse passo ta aqui só pra eu mostrar pra vocês o quão lindo não fica graficamente isso tudo :D