a) Apresente a extensão ímpar e periódica de período de :
b) Encontre a série de Fourier de senos da função do item (a)
Passo 1
a) Vamos começar montando o gráfico de uma função ímpar a partir de . Esse é o gráfico de :
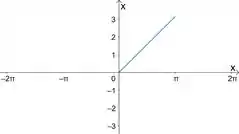
Para a gente montar uma função ímpar a partir dele, precisamos espelhar esse gráfico em relação ao eixo . E o gráfico que resultar disso, a gente espelha em relação ao eixo :

Daí, nossa função ímpar tem essa definição:
E como nosso período vale , dizemos que
Tá aí a definição da nossa extensão!
Passo 2
b) Para encontrar a série de Fourier de senos para essa função, a gente só precisa usar a fórmulinha
Do enunciado a gente viu que . Então
Aí só falta calcular que tem essa carinha:
Já que e
Bora calcular essa integral!
Passo 3
Como a gente tem o produto entre duas funções, podemos usar integração por partes:
Jogando na fórmulinha de integração por partes, a gente tem
Passo 4
Daí a gente tem que
Como esse cosseno fica alternando entre 0 e 1 conforme , um número inteiro, aumenta, podemos escrever que
Aí nossa continha fica:
E a série de Fourier fica:
Resposta
a) com
b)