Seja a função definida por
a) Determine a série de Fourier em senos de
b) Esboce o gráfico da série de Fourier, obtida no item anterior, no intervalo
c) Calcule o valor da série
Passo 1
Para resolver isso vamos, vamos encontrar o coeficiente da série de Fourier, mas perceba que como somente é a série em senos, só precisamos saber .
Assim, temos que:
Substituindo:
Passo 2
Beleza, agora vamos resolver isso aí.
A integral:
Então:
E:
Juntando tudo:
Agora vamos analisar o valor de em relação a paridade de . Vamos lá
Quando é par, logo
Quando é ímpar,
Assim, temos:
Passo 3
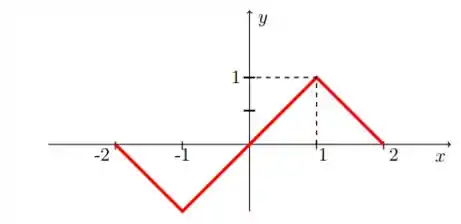
b)
Agora vamos plotar o gráfico. Esse gráfico é bem simples, no intervalo de ele ficará como:
Passo 4
c)
Perceba que esse valor aparece no somatório. Basta escolhermos um valor para x para que o tenhamos somente constantes acompanhadas de
Tomando temos:
Logo temos que: