Funções pares e ímpares e desigualdade de bessel e identidade de Parseval
Sendo
- Determine a série de Fourier de cossenos da função
- Esboce o gráfico da função .
- Determine e
Passo 1
b)
Vamos começar fazendo o gráfico, para a gente poder visualizar melhor a questão, ok? Primeiro, vamos desenhar os dados do enunciado:
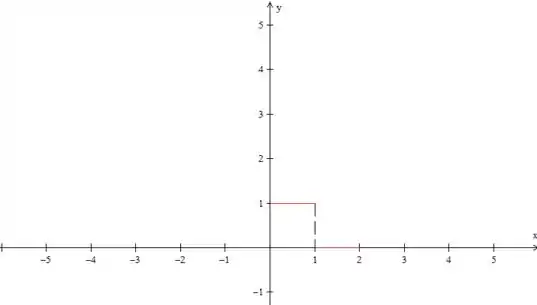
Até aqui nada demais, né? Como a questão pede uma série de cossenos, temos que fazer uma extensão par dessa função. Então, o próximo passo é espelhar isso que desenhamos do eixo , dessa forma:
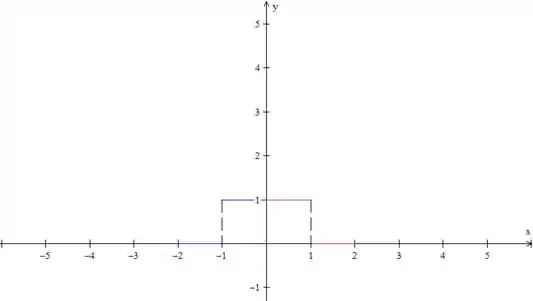
Bom, a função tem que ser periódica, né? Então vamos repetir esse padrão, para a esquerda e para a direita.
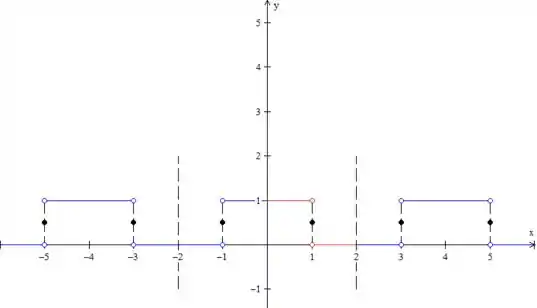
Pronto, temos então três períodos da função, como pede o enunciado. É bom você sempre desenhar esse tracejado grande para marcar o período da função, para não se perder!
Repare nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de salto, a função vale a média dos limites laterais. Nesse caso:
Nós colocamos então as bolinhas cheias em (repare que todas as retas tem bolinhas vazias nas suas extremidades).
Passo 2
a)
Beleza, agora temos que representar a função em série de Fourier. Como temos uma série de cossenos:
Passo 3
Agora vamos calcular
Fazendo na expressão de :
Agora temos que dividir essa integral em duas, pois vale em e vale em , temos então
Assim:
Passo 4
Agora vamos calcular os outros ’s. Temos que:
Dividindo essa integral em duas, como fizemos com :
Agora vamos analisar esse seno com calma.
Se é par, ou seja, se
Logo
Agora vamos analisar os ’s ímpares, fazendo , temos:
Logo, para ímpar, sendo
Então, podemos dizer que
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Vamos substituir agora o coeficiente . Repare que para , se anula, então só estamos interessados nos ’s ímpares, quando . Vamos então substituir isso na série.
Fazendo :
Para temos , portanto a série deve começar em .Temos então
Passo 6
c)
Vamos agora achar os valores que ele pediu e
Lembrando que
Temos que ver o qual o equivalente a cada um desses valores que ele pediu de entre e
Vamos começar com
Lembrando que , temos que ver entre quais dois múltiplos impares disso ele está.
Temos
Vamos agora passar isso para à , para isso vamos subtrair em toda a equação
Fazendo uma aproximação temos
E
Então
E vamos ter
Passo 7
Vamos para com
Dessa vez já temos um múltiplo ímpar de , assim temos que o seu valor vai ser
Resposta
a)
b)
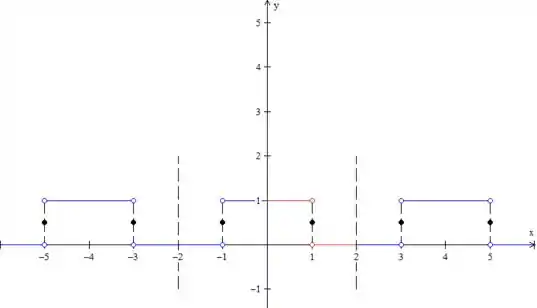
c)