Seja a função definida por:
- Determine a série de Fourier em senos de .
- Esboce o gráfico da série obtida no item (a) no intervalo
- Calcule o valor da série:
Passo 1
OK, vamos começar com a letra (a). Para determinar a série de Fourier precisamos que a função seja periódica. Então, vamos fazer a extensão ímpar desta função. Vamos lá?
Não precisamos determinar por agora qual a expressão da extensão ímpar, que chamaremos de , vamos só considerar duas coisas.
O período da função vai ser duas vezes o intervalo dado. Como vai de , então a extensão será -periódica. Além disso, como estamos fazendo a extensão ímpar teremos uma série só de senos, ficando:
Como a extensão é -periódica e a fórmula geral é periódica, então temos e:
Show. Agora vamos determinar esse coeficiente. Pela fórmula geral, vamos ter:
Como a nossa extensão é impar e a função seno também é ímpar, o integrando será par. Portanto:
Para o intervalo de , a extensão vai ser exatamente igual a própria função, portanto:
Separando em uma integral para cada expressão:
Assim, teremos:
Assim, vamos ter:
Passo 2
Agora, vamos para a letra (b). Para esboçarmos o gráfico da extensão ímpar, precisamos determinar a expressão da extensão ímpar .
A parte positiva de para de será idêntica a , com exceção dos pontos de mudança de expressão, que veremos mais para frente. Então teremos:
Vamos colocar isso no nosso esboço:
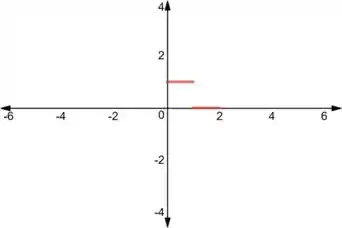
Agora, para a parte negativa, como estamos fazendo uma extensão ímpar, precisamos que:
Portanto, vamos ter:
Que é justamente a condição que satisfaz . Vamos colocar isso no gráfico também:
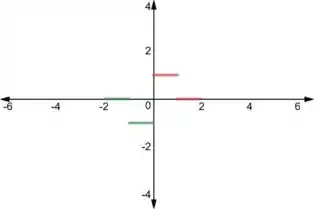
Agora, precisamos que a função seja periódica e com o período igual ao intervalo que definimos. Então, vamos ter:
Isso significa que repetimos o nosso gráfico a cada 4 unidades. Fazendo isso:
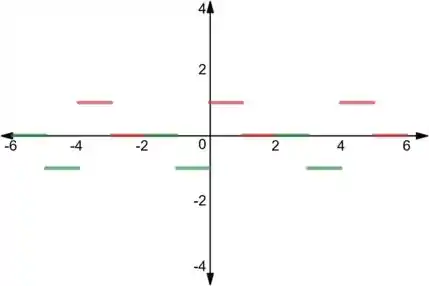
Para completar nossa extensão, vamos ver os pontos em que a função muda de expressão. Nesses pontos, pelo teorema de convergência da série de Fourier, a série vai convergir para a média dos limites laterais, ou seja, teremos:
OK. Já temos o que precisamos. A expressão da extensão então vai ser:
Marcamos então os pontos que ficaram faltando sem esquecer de repeti-los de acordo com o período da função:
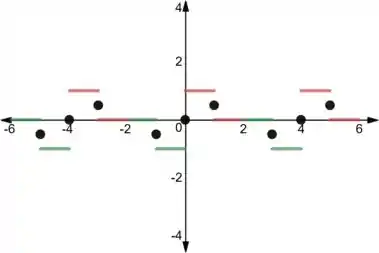
Show. Esse vai ser o gráfico.
Passo 3
Agora vamos para letra (c). A questão tá pedindo o valor de
Para chegar nesse valor, vamos tentar deixar a série que obtemos na forma da série pedida. Temos no momento:
Bem, fazendo , temos:
Distribuindo, vamos ter:
Temos que:
Assim, vamos ter:
Só que uma coisa aí. Como é um número inteiro, pelo círculo trigonométrico:
Pois estamos sempre andando pelos valores:
Assim, teremos:
Vamos analisar agora o:
Toda vez que for um número par, teremos:
Assim, mudamos o índice para englobando somente valores ímpares:
Quando , . Logo, mudando o contador também ficando:
Já está parecido com a série que queremos:
Olhando para o nosso seno, temos:
Como:
Portanto, vamos ter:
Quase lá! Vendo agora o cosseno, vamos ter:
Portanto:
Logo:
Se você não se lembra da relação acima, é muito importante gravar. 😉
Beleza. Assim, a série vai ser:
Ou seja:
Vimos na letra (b) que, pelo teorema de convergência da série de Fourier:
Logo:
E é essa a série que o problema pediu. Não faz diferença usarmos e não , o resultado não muda por isso.
Resposta
(a)
(b) 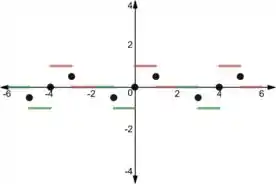
(c)