Seja
a)Determine a série de Fourier de senos de
b)Mostre que a série de Fourier de senos de converge para uma função e esboce o gráfico da função em
c)Determine
Passo 1
a)Calma galera, você pode estar pensando, mas cara, essa função é par!!! Como fazer ela como uma série de Fourier de seno se essa série só existe pra função ímpar? Mas opa, ele só definiu a função de , se a gente definir em , pronto esse moleque é ímpar!
Bem bem, a série de Fourier de seno é:
]
:
A segunda integral vamos resolver de forma indeterminada primeiro, ela é maiorzinha:
Vamos fazer uma integração por partes:
Assim fica:
Agora para resolver essa outra integral, novamente outra integração por partes:
Então simbora:
Desenvolvendo:
Então vimos que:
Substituindo:
Mas:
Assim finalmente:
]
E com isso a série de Fourier de seno fica definida:
Passo 2
b)A extensão dessa função é seccionalmente contínua, e seccionalmente de classe , logo pelo teorema de convergência da série de Fourier, esta série converge a toda extensão em , exceto nos pontos de descontinuidade!
Então a função fica assim:
E é só repetir o período que não tem erro!
O gráfico ficou:
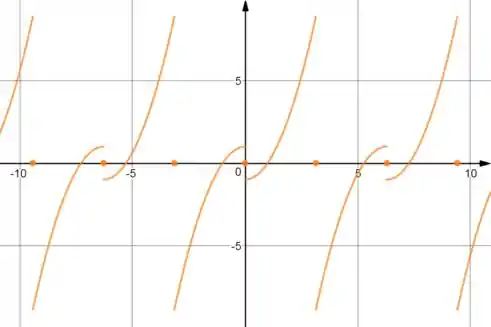
Passo 3
c)
Ae tu fica, “É clã, soldado morreu na trincheira” Mas calma, lembra que isso é uma função periódica e uma função ímpar, a cada 1 período a área necessariamente tem que dar zero!, vamos reescrever isso:
Para facilitar mais ainda, podemos tirar mais coisa:
Mas opa, a gente viu que dentro de a função que rege isso é:
Logo:
Resposta
a)
b) A extensão dessa função é seccionalmente contínua, e seccionalmente de classe , logo pelo teorema de convergência da série de Fourier, esta série converge a toda extensão em , exceto nos pontos de descontinuidade
c)