Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Série de Fourier apenas em senos ou cossenos

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536373839404142434445464748495051525354555657

Enunciado

Seja f a função definida por

f x = x 2 , x ∈ [ 0 , π ]

Analise as seguintes afirmações:

1 A série em senos de f é

∑ n = 1 ∞ - 1 n + 1 sen ⁡ n x n

( 2 ) A série de cossenos de f é

π 4 + ∑ n = 1 ∞ - 1 n cos ⁡ n x n 2 π

( 3 ) A série de cossenos de f para x = π converge para π 2

Podemos afirmar que:

( a ) 1 ,   2   e   ( 3 ) são verdadeiras

( b ) Apenas ( 1 ) e ( 3 ) são verdadeiras

( c ) Apenas ( 2 ) e ( 3 ) são verdadeiras

( d ) Apenas ( 1 ) é verdadeira

( e ) Apenas 3 é verdadeira

Passo 1

Vamos começar analisando a primeira afirmativa:

1 A série em senos de f é

∑ n = 1 ∞ - 1 n + 1 sen ⁡ n x n

Dado que L = π , isso quer dizer que ele afirma que

b n = - 1 n + 1 n

Vamos ver se isso é verdade. Sabendo que:

b n = 2 L ∫ 0 L f x sen ⁡ n x d x

E tendo que f x = x 2 e L = π :

b n = 2 π ∫ 0 π x 2 sen ⁡ n x d x

b n = 1 π ∫ 0 π x sen ⁡ n x d x

Passo 2

Aqui vamos usar a integração por partes. Lembra da fórmula? Olha só:

∫ u d v = u v - ∫ v d u

Chamando:

u = x → d u = d x

d v = sen ⁡ n x d x → v = - 1 n cos ⁡ n x

Então ficamos com:

1 π ∫ 0 π x sen ⁡ n x d x = 1 π - x n cos ⁡ n x 0 π + 1 n ∫ 0 π cos ⁡ n x d x

1 π ∫ 0 π x sen ⁡ n x d x = 1 π - π n cos ⁡ n π + 0 n cos ⁡ 0 + 1 n 1 n sen ⁡ n x 0 π

Sabendo que cos ⁡ π n = - 1 n

1 π ∫ 0 π x sen ⁡ n x d x = 1 π - π n - 1 n + 1 n 2 sen ⁡ π n - sen ⁡ 0

1 π ∫ 0 π x sen ⁡ n x d x = 1 π π n - 1 n + 1

1 π ∫ 0 π x sen ⁡ n x d x = - 1 n + 1 n

Então a afirmativa é verdadeira.

Passo 3

Agora analisando a segunda afirmativa:

( 2 ) A série de cossenos de f é

π 4 + ∑ n = 1 ∞ - 1 n cos ⁡ n x n 2 π

Dado que L = π , isso quer dizer que ele afirma que

a n = - 1 n n 2 π

a 0 = π 2

Vamos ver se isso é verdade. Sabendo que:

a 0 = 2 L ∫ 0 L f x d x

a n = 2 L ∫ 0 L f x cos ⁡ n x d x

E tendo que f x = x 2 e L = π :

Vamos aplicar essas integrais no nosso caso:

a 0 = 2 π ∫ 0 π x 2 d x = x 2 2 π 0 π = π 2

Beleza, até agora a alternativa pode ser verdadeira. Vamos ver o a n .

a n = 2 π ∫ 0 π x 2 cos ⁡ n x d x

a n = 1 π ∫ 0 π x cos ⁡ n x d x

Passo 4

Resolvendo essa integral:

∫ u d v = u v - ∫ v d u

Chamando:

u = x → d u = d x

d v = cos ⁡ n x d x → v = 1 n sen ⁡ n x

Então ficamos com:

1 π ∫ 0 π x cos ⁡ n x d x = 1 π x n sen ⁡ n x 0 π + 1 n ∫ 0 π sen ⁡ n x d x

1 π ∫ 0 π x cos ⁡ n x d x = 1 π π n sen ⁡ n π + 0 n sen ⁡ 0 + 1 n - 1 n cos ⁡ n x 0 π

1 π ∫ 0 π x cos ⁡ n x d x = 1 π - 1 n 2 cos ⁡ n x 0 π = - 1 π n 2 cos ⁡ π n - cos ⁡ 0

Sabendo que cos ⁡ π n = - 1 n

1 π ∫ 0 π x cos ⁡ n x d x = - 1 π n 2 - 1 n - 1

1 π ∫ 0 π x cos ⁡ n x d x = 1 - - 1 n π n 2

Então:

a n = 1 - - 1 n π n 2

E a alternativa é falsa mesmo.

Passo 5

Finalmente, analisando a última afirmativa:

3 A série de cossenos de f para x = π converge para π 2

Bom, a série em cossenos é a extensão par da função, é só refleti-la no eixo y e repeti-la quantas vezes quiser. Dá uma olhada:

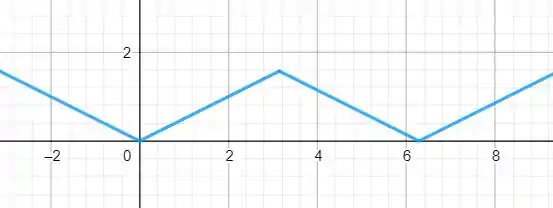
Pelo Teorema da Convergência da série de Fourier e como a função é contínua em x = π

Temos que S π = f π = π 2

Ou seja, converge para π 2 .

A afirmativa é verdadeira!

Resposta

( b ) Apenas ( 1 ) e ( 3 ) são verdadeiras

Exercícios de Livros Relacionados

(a) Sejam v 1 ,v 2 e v 3 três vetores ortogonais dois a dois em três dimensões, e seja u qualquer vetor tridimensional. Mostre que u = a 1 v 1 + a 2 v 2 + a 3 v 3 , Em que a i = u ∙ v i v i ∙ v i , i
f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função
Considere a função f definida no problema 21, e seja e m = f x - s m ( x ) . f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Faça o gráfico de e m ( x ) em função de x para 0 ≤ x ≤ 2 para diversos valores
f x = x ,- 1 ≤ x1 f x + 2 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função de
Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. x 2