- Determine a série de Fourier em cossenos da função:
Passo 1
Letra a)
Vamos começar fazendo o gráfico dessa função. Como o problema pede uma série de cossenos, sabemos que queremos uma extensão par de , certo?
Então, desenhamos em (em vermelho), espelhamos esse desenho em relação a (em azul) e repetimos esse período (em verde):
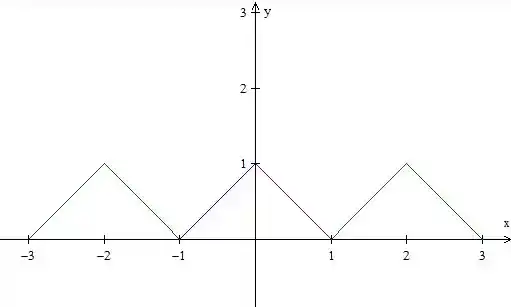
Passo 2
Beleza, agora vamos montar o problema. Como a função é par, temos o seguinte:
Como o período dessa função é , temos ,esse é intervalo em que ela se repete. Lembra que a função representada por Série de Fourier tem que ser periódica? Então
Passo 3
Agora vamos calcular
Fazendo na expressão de e , temos:
Como em , temos:
Logo
Passo 4
Agora vamos calcular os outros ’s. Temos que:
O que nos dá
Agora vamos fazer a integração por partes:
Como
Podemos escrever então
Guarde isso!
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Deixamos o por último que é mais chatinho.
Não podemos escrever direto no somatório porque isso só vale para ímpar! Vamos definir então , porque isso garante que temos índices ímpares, ok? Para temos , portanto a série deve começar em . Temos então
Você pode poderia ter definido , porém, nesse caso, o somatório iria começar em .