Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Série de Fourier apenas em senos ou cossenos

Ver Teoria
Exercício 311234567891011121314151617181920212223242526272829303233343536373839404142434445464748495051525354555657

Enunciado

Seja f x = x 2 ,   [ 0,1 ] 0 ,     ( 1,2 ]

(a) Ache a série de senos S x da f x

(b) Ache a soma da série de senos e esboce o seu gráfico no intervalo [-6,6].

(c) Ache S ( - 321 ) .

Passo 1

A questão está pedindo pra gente achar a série de senos da f ( x ) , né? Então, vamos lembrar que a série de Fourier é da seguinte forma:

f x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n π x L + ∑ n = 1 ∞ b n sen ⁡ n π x L

Como a questão pediu apenas a série de senos, então vamos precisar apenas de:

f x = ∑ n = 1 ∞ b n s e n ⁡ n π x L

Aí vai ficar assim:

b n = 2 L ∫ 0 1 x 2 sen ⁡ n π x 2 + ∫ 1 2 0 sen ⁡ n π x 2

b n = ∫ 0 1 x 2 sen ⁡ n π x 2

Passo 2

Vamos agora resolver essaintegral para descobrimos o b n .

Bom, essa integral a gente resolve com integração por partes duas vezes.

Lembra da fórmula?

∫ u . d v = u . v - ∫ v . d u

e vamos chegar a:

b n = - 2 x 2 n π cos ⁡ n π x 2 + 8 x n π 2 sen ⁡ n π x 2 + 16 n π 3 cos ⁡ n π x 2 0 1

Já com o intervalo. Lembra que de 1 a 2 a função vale zero? Por isso que não entrou aqui, ok?

Agora, substituindo os valores dos intervalos, vamos ter:

b n = - 2 n π cos ⁡ n π 2 + 8 n π 2 sen ⁡ n π 2 + 16 n π 3 cos ⁡ n π 2 - 16 n π 3

b n = 2 8 - n π 2 n π 3 cos ⁡ n π 2 + 4 n π 2 sen ⁡ n π 2 - 8 n π 3  

Passo 3

UFAA!Chegamos no valor de b n , agora vamos substituir para acharmos a nossa função de senos:

f x = ∑ n = 1 ∞ b n s e n ⁡ n π x L

f x = ∑ n = 1 ∞ 2 8 - n π 2 n π 3 cos ⁡ n π 2 + 4 n π 2 sen ⁡ n π 2 - 8 n π 3   s e n ⁡ n π x L

Passo 4

Agora vamos para o item (b). Que tal mudar um pouco a ordem e começar pelo gráfico da função. Ele pode nos ajudar a entender melhor a função depois.

f x = x 2 ,     [ 0,1 ] 0 ,     ( 1,2 ]

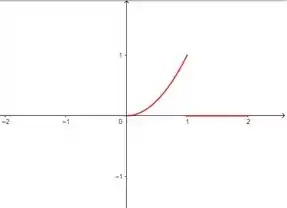
Como a questão pediu uma série de senos, então precisamos de uma função ímpar. Então, vamos fazer a extensão ímpar da função. Para isso, vamos começar espelhando a função em relação ao eixo y :

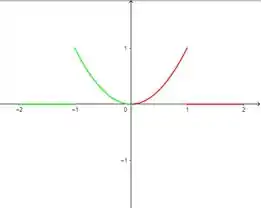
Essa parte verde é a parte espelhada. Agora, vamos espelhar a parte verde em relação ao eixo x , da seguinte forma:

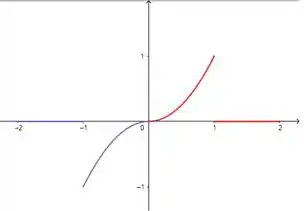
Pronto, agora temos a nossa função com extensão ímpar.

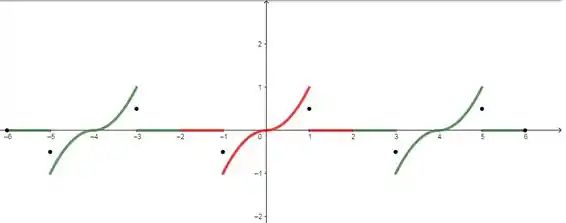
Agora, só precisamos repetir o período para poder desenhá-la no intervalo [ - 6,6 ] .

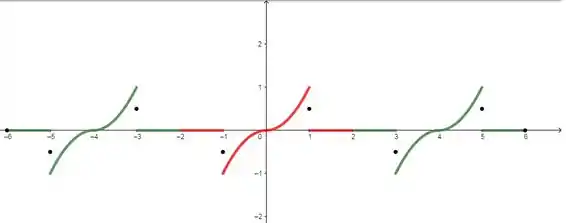
A parte vermelha é a função com extensão ímpar enquanto que a parte verde é a repetição do período. Repare que nos pontos de continuidade a função vale a média dos limites laterais, já que estamos representando a função para a qual a série de Fourier converge.

Passo 5

Bom, agora vamos resolver a soma da série dos senos.

Como fizemos uma extensão ímpar da função, temos que:

f x = - f ( - x )

Além disso, nos pontos de descontinuidade a função assume o valor da mpedia dos limites laterais. Beleza, como vai ficar então?

f ¯ x = 0 ,     - 2 ≤ x < - 1 - 1 2 ,     x = - 1                     - x 2 ,     - 1 < x ≤ 0 x 2 ,     0 ≤ x < 1 1 2 ,     x = 1                 0 ,     1 < x ≤ 2

Agora, vamos escrever a soma S ( x ) , que vai ser essa f ¯ ( x ) estendida para qualquer valor de x . Repara que se somarmos 4 no valor de x   , o valor da função em x + 4 não muda. (Se preferir, volta um pouquinho e testa lá no gráfico para ficarmais claro), ou seja...

S x = S ( x + 4 )

Assim, a nossa função fica com essa carinha:

S x = S ( x + 4 k )

Onde k é um número inteiro.

A soma no intervalo de - 2 a 2 vai ser a própria f ¯ ( x )

Então, agora é só pegar a nossa f ¯ ( x ) e somar nos intervalos o 4 k .

S x = 0 ,     - 2 + 4 k ≤ x < - 1 + 4 k - 1 2 ,     x = - 1   + 4 k                                     - x 2 ,     - 1 + 4 k < x ≤ 0 + 4 k   x 2 ,     0 + 4 k ≤ x < 1 + 4 k 1 2 ,     x = 1 + 4 k                                       0 ,     1 + 4 k < x ≤ 2 + 4 k

Passo 6

Shoow! Agora vamos resolver a letra (c). A questão pediu

S ( - 321 )

Para isso, precisamos descobrir em intervalo esse - 321 está na nossa fórmula da S ( x ) .

Podemos pensar em qual é o múltiplo de 4 mais próximo desse valor. Um macete para acharmos um múltiplo de 4 é que os dois últimos algorismo do número também forma um múltiplo de 4. Por exemplo, -320. Os dois últimos algorismo forma 20, que é um múltiplo de 4.

Então, o nosso - 321 é da forma:

- 321 = - 1 + 4 k

Lembrando que como k é um número inteiro, isso significa que ele pode assumir valores positivos e negativos, ok

Voltando na nossa S x , a gente vê que para - 1 + 4 k , a S - 1 + 4 k = - 1 2

Logo, chegamos a nossa soma.

S - 321 = - 1 2

Resposta

(a) f x = ∑ n = 1 ∞ 2 8 - n π 2 n π 3 cos ⁡ n π 2 + 4 n π 2 sen ⁡ n π 2 - 8 n π 3   s e n ⁡ n π x L

(b) S x = 0 ,     - 2 + 4 k ≤ x < - 1 + 4 k - 1 2 ,     x = - 1   + 4 k                                     - x 2 ,     - 1 + 4 k < x ≤ 0 + 4 k   x 2 ,     0 + 4 k ≤ x < 1 + 4 k 1 2 ,     x = 1 + 4 k                                       0 ,     1 + 4 k < x ≤ 2 + 4 k

(c) S - 321 = - 1 2

Exercícios de Livros Relacionados

(a) Sejam v 1 ,v 2 e v 3 três vetores ortogonais dois a dois em três dimensões, e seja u qualquer vetor tridimensional. Mostre que u = a 1 v 1 + a 2 v 2 + a 3 v 3 , Em que a i = u ∙ v i v i ∙ v i , i
f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função
Considere a função f definida no problema 21, e seja e m = f x - s m ( x ) . f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Faça o gráfico de e m ( x ) em função de x para 0 ≤ x ≤ 2 para diversos valores
f x = x ,- 1 ≤ x1 f x + 2 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função de
Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. x 2