Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Série de Fourier apenas em senos ou cossenos

Ver Teoria
Exercício 351234567891011121314151617181920212223242526272829303132333436373839404142434445464748495051525354555657

Enunciado

( a ) Determine a série de Fourier em cossenos da função

f x = 0   s e   0 ≤ x < 1 x - 1 2   s e   1 ≤ x ≤ 2

( b ) Esboce o gráfico da série de Fourier obtida em ( a ) no intervalo [ - 6,6 ] .

( c ) Calcule o valor da série

∑ m = 1 ∞ - 1 m + 1 m 2

Passo 1

( a )

Fazendo a extensão par da função:

g x = f x ,     s e   0 ≤ x ≤ 2 f - x ,     s e - 2 ≤ x ≤ 0 g ( x + 4 )

Logo, a série de Fourier associada (em termos de cossenos) é da forma:

S x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n π x 2

Passo 2

Onde

a 0 = 2 2 ∫ 0 2 f x d x = ∫ 1 2 x - 1 2 d x = ∫ 1 2 x 2 - 2 x + 1 d x = x 3 3 - x 2 + x 1 2

= 7 3 - 2 = 1 3

Passo 3

a n = 2 2 ∫ 0 2 f x cos ⁡ n π x 2 d x = ∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x

Aqui vamos usar a integração por partes. Lembra da fórmula?

∫ u d v = u v - ∫ v d u

Chamando

u = x - 1 2 → d u = 2 x - 1 d x

d v = cos ⁡ n π x 2 d x → v = 2 n π sen ⁡ n π x 2

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = 2 x - 1 2 n π sen ⁡ n π x 2 1 2 - ∫ 1 2 2 x - 1 2 n π sen ⁡ n π x 2 d x

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = 2 2 - 1 2 n π sen ⁡ n π 2 2 - 2 1 - 1 2 n π sen ⁡ n π 1 2 - 4 n π ∫ 1 2 x - 1 sen ⁡ n π x 2 d x

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = - 4 n π ∫ 1 2 x - 1 sen ⁡ n π x 2 d x

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = - 4 n π ∫ 1 2 x sen ⁡ n π x 2 d x - ∫ 1 2 sen ⁡ n π x 2 d x

Vamos usar integração por partes novamente naquele ∫ 1 2 x sen ⁡ n π x 2 d x :

u = x → d u = d x

d v = sen ⁡ n π x 2 d x → v = - 2 n π cos ⁡ n π x 2

∫ 1 2 x sen ⁡ n π x 2 d x = - 2 x n π cos ⁡ n π x 2 1 2 + 2 n π ∫ 1 2 cos ⁡ n π x 2 d x

∫ 1 2 x sen ⁡ n π x 2 d x = - 4 n π cos ⁡ n π + 2 n π cos ⁡ n π 2 + 4 n 2 π 2 sen ⁡ n π x 2 1 2

∫ 1 2 x sen ⁡ n π x 2 d x = - 4 n π c o s ⁡ ( n π ) + 4 n 2 π 2 sen ⁡ n π - 4 n 2 π 2 sen ⁡ n π 2

∫ 1 2 x sen ⁡ n π x 2 d x = - 4 n π c o s ⁡ ( n π ) - 4 n 2 π 2 sen ⁡ n π 2

Voltando com esse valor pra nossa integral:

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = - 4 n π - 4 n π c o s ⁡ ( n π ) - 4 n 2 π 2 sen ⁡ n π 2 - ∫ 1 2 sen ⁡ n π x 2 d x

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = 4 n π 4 n π cos ⁡ n π + 4 n 2 π 2 sen ⁡ n π 2 - 2 x n π cos ⁡ n π x 2 1 2

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = 4 n π 4 n π cos ⁡ n π + 4 n 2 π 2 sen ⁡ n π 2 - 2 x n π cos ⁡ n π x 2 1 2

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = 4 n π 4 n π cos ⁡ n π + 4 n 2 π 2 sen ⁡ n π 2 - 2 n π cos ⁡ n π + 2 n π cos ⁡ n π 2

∫ 1 2 x - 1 2 cos ⁡ n π x 2 d x = 4 n π 2 n π cos ⁡ n π + 4 n 2 π 2 sen ⁡ n π 2

= 2 n π 4 n π cos ⁡ n π + 8 n 2 π 2 sen ⁡ n π 2 ,     n ≥ 1

Passo 4

( b )

Nossa função é essa:

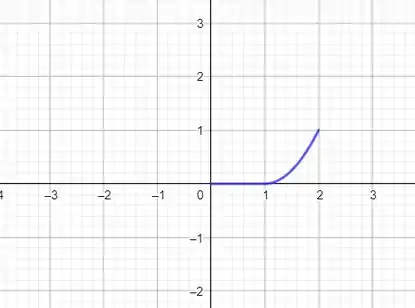
Como estamos fazendo a extensão par, vamos refleti-la no eixo y :

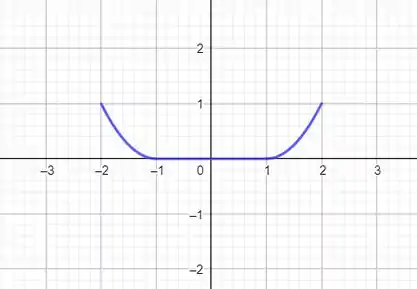
Agora é só repetir isso no intervalo [ - 6,6 ] :

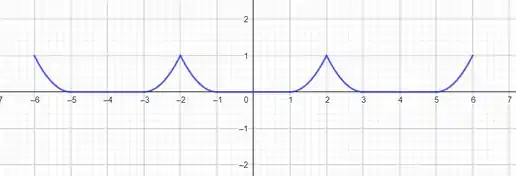
Prontinho! É assim que ela fica!

Passo 5

( c )

Bom, a representação da nossa função em série de Fourier é:

f x = 1 6 + ∑ n = 1 ∞ 2 n π 4 n π cos ⁡ n π + 8 n 2 π 2 sen ⁡ n π 2 cos ⁡ n π x 2

f 1 = 1 6 + ∑ n = 1 ∞ 2 n π 4 n π cos ⁡ n π + 8 n 2 π 2 sen ⁡ n π 2 cos ⁡ n π 2

0 = 1 6 + ∑ n = 1 ∞ 2 n π 4 n π cos ⁡ n π + 8 n 2 π 2 sen ⁡ n π 2 cos ⁡ n π 2

Mas

cos ⁡ n π 2 = 0 s e n = í m p a r - 1 n s e n = p a r

Lembrando que, se temos uma série, ela pode ser reescrita como

∑ n = 1 ∞ c n = ∑ k = 1 ∞ c 2 k + ∑ k = 1 ∞ c 2 k + 1

Se n = í m p a r , o somatório fica

∑ k = 1 ∞ 2 2 k + 1 π 4 2 k + 1 π cos ⁡ 2 k + 1 π + 8 2 k + 1 2 π 2 sen ⁡ 2 k + 1 π 2 cos ⁡ 2 k + 1 π 2

Mas esse termo é 0 .

Se n = p a r , o somatório fica

∑ k = 1 ∞ 2 2 k π 4 2 k π cos ⁡ 2 k π + 8 2 k 2 π 2 sen ⁡ 2 k π 2 cos ⁡ k π

∑ k = 1 ∞ 2 2 k π 4 2 k π cos ⁡ 2 k π + 8 2 k 2 π 2 sen ⁡ k π cos ⁡ k π

Podemos fazer

cos ⁡ k π = - 1 k

cos ⁡ 2 k π = 1

sen ⁡ k π = 0

Essa série vai ficar

∑ k = 1 ∞ 8 4 k 2 π 2 - 1 k

∑ k = 1 ∞ 2 - 1 k k 2 π 2

Assim, a nossa série vai ficar:

∑ n = 1 ∞ 2 n π 4 n π cos ⁡ n π + 8 n 2 π 2 sen ⁡ n π 2 cos ⁡ n π 2 = ∑ k = 1 ∞ 2 2 k π 4 2 k π cos ⁡ 2 k π + 8 2 k 2 π 2 sen ⁡ 2 k π 2 - 1 k

E a nossa expressão lá de cima fica

0 = 1 6 + ∑ k = 1 ∞ 2 - 1 k k 2 π 2

∑ k = 1 ∞ 2 - 1 k k 2 π 2 = - 1 6

Olhaaaaa, que beleza. Quase achamos a série, vamos fazer os ajustes para achar a série que ele pediu:

  1. Multiplicando tudo por - 1 para termos - 1 k + 1

    2. ∑ k = 1 ∞ 2 - 1 k + 1 k 2 π 2 = 1 6

  2. Agora passamos o 2 π 2 para o outro lado

∑ k = 1 ∞ - 1 k + 1 k 2 = π 2 12

Resposta

a   f x = 1 6 + ∑ n = 1 ∞ 2 n π 4 n π cos ⁡ n π + 8 n 2 π 2 sen ⁡ n π 2 cos ⁡ n π x 2

b  

c   ∑ k = 1 ∞ - 1 k + 1 k 2 = π 2 12

Exercícios de Livros Relacionados

(a) Sejam v 1 ,v 2 e v 3 três vetores ortogonais dois a dois em três dimensões, e seja u qualquer vetor tridimensional. Mostre que u = a 1 v 1 + a 2 v 2 + a 3 v 3 , Em que a i = u ∙ v i v i ∙ v i , i
f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função
Considere a função f definida no problema 21, e seja e m = f x - s m ( x ) . f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Faça o gráfico de e m ( x ) em função de x para 0 ≤ x ≤ 2 para diversos valores
f x = x ,- 1 ≤ x1 f x + 2 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função de
Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. x 2