Séries de Fourier, Séries de Fourier- funções pares e ímpares
- Considere a função de período definida por , para . Determinar a série de Fourier da função .
- Usando o item (a), calcular a soma da série . Justifique a sua resposta.
Passo 1
A primeira coisa que você vai fazer em uma questão de série de Fourier é desenhar o gráfico de , mesmo que o enunciado não peça. Porque só assim podemos descobrir se é uma função par ou ímpar (ou nenhuma das duas), o que pode facilitar muito nossa vida!
Temos então:
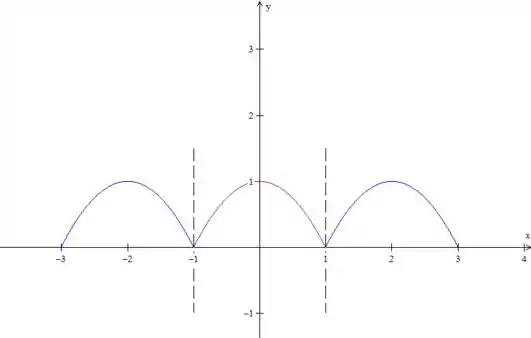
Primeiro desenhamos a definição de que está nos colchetes no enunciado (em vermelho). Depois repetimos esse padrão a cada intervalo de em , pois esse é o seu período. É bom você sempre desenhar esse tracejado para marcar o período da função!
Bom, já deu para perceber que é uma função do tipo par, né? Ela é espelhada em .
Passo 2
Beleza, agora vamos montar o problema. Como a função é par, temos o seguinte:
Como , sabemos que o período da função é esse é intervalo em que ela se repete. Lembra que a função representada por Série de Fourier tem que ser periódica? Então
Passo 3
Agora vamos calcular
Fazendo na expressão de e , temos:
Como , temos:
Logo
Passo 4
Agora vamos calcular os outros ’s. Temos que:
O que nos dá
Como temos que
Podemos escrever:
Logo
Se não houver formulário, você tem que calcular essa integral do braço mesmo! Infelizmente :P Mas então chegamos a
Sabemos que
Então temos o seguinte
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Passo 6
Letra b)
Agora o problema pede para calcularmos a soma da série
Ok, o que isso tem a ver com a questão?! Aparentemente nada, mas vamos olhar com mais calma. Vamos chamar essa soma de , beleza?
Repara no seguinte:
Esse é o nosso resultado do item (a). Agora olha o que acontece quando fazemos
Como é contínua em , pelo Teorema da convergência de Fourier, sabemos que a soma da série é igual ao valor da função naquele ponto. Caso houvesse descontinuidade, a série seria igual à média dos limites laterais da função no ponto em questão!
Bom, apareceu a soma que queremos ali, né? Concluímos que:
E nós sabemos, pelo próprio problema, que
Logo
O que nos dá