Seja a função definida por
- Seja a extensão ímpar e periódica de período da função . Esboce o gráfico de no intervalo .
- Encontre a série de Fourier de .
Passo 1
Temos aqui uma função de uma variável arbitrária em um intervalo que leva aos reais, definida pela forma funcional
A primeira alternativa quer a extensão ímpar de período 2 desta função, e que façamos o seu esboço! Isto será necessário para que calculemos a série de Fourier na alternativa b).
Vamos começar escrevendo a extensão ímpar periódica e esboçando o gráfico desta função! Após, utilizaremos a definição de Série de Fourier para resolver a segunda alternativa! Vem comigo!
Passo 2
Temos que a nossa função definida em tem o seguinte comportamento
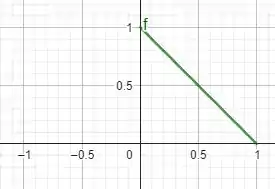
Se lembrarmos que por definição, uma função ímpar respeita a propriedade , temos que
E como, precisamos que , temos que a extensão ímpar será
definida no intervalo . Ou seja, temos que é definida tal que
O gráfico desta extensão ímpar no intervalo tem a forma
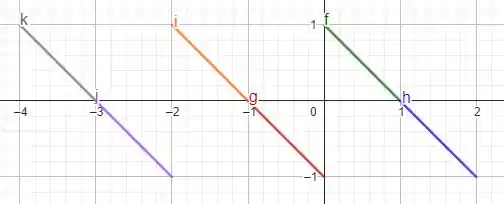
Esta é a primeira alternativa! Agora vamos calcular a série de Fourier desta função! Note que esta é uma função ímpar! Portanto, a série será uma série de senos! Você lembra o que isso quer dizer? Se não, vamos relembrar agorinha mesmo!
Passo 3
Temos que uma série de Fourier é definida tendo em vista a seguinte expansão
em que podemos calcular os coeficientes utilizando as seguintes expressões
O fato de que é uma função ímpar, facilita a nossa vida um bocado! Note que integrais de funções ímpares em intervalos simétricos são nulas! E, também lembre que se fizermos o produto de uma função par com uma função ímpar, temos uma função ímpar! Mas, se fizermos o produto de duas funções ímpares, temos uma função par. Isso é importante por quê? Note que em nosso caso, temos que , e temos que é ímpar. Você consegue afirmar algo sobre as integrais para os coeficientes tendo isso em mente? Vem comigo!
Passo 4
Vamos começar com , temos que
Como temos um intervalo simétrico e é ímpar, temos que . Agora, vamos analisar o coeficiente , temos que
Como é ímpar e é uma função par, temos que seu produto é uma função ímpar! Como nosso intervalo é simétrico, podemos garantir que . Só nos resta , temos que
Agora temos que é ímpar e também é ímpar, então o produto de ambas as funções é uma função par! Ou seja, no intervalo a integral não se anula, mas, pode ser reescrita como
Nosso problema se resume agora em resolver a integral para este coeficiente! Bora lá!
Passo 5
Note que no intervalo da integral, temos que , portanto, temos que
tudo que fiz foi aplicar a distributiva no parênteses e separar em duas integrais! A primeira integral pode ser identificada diretamente como uma integral conhecida, a segunda no entanto vai precisar ser integrada por partes! O primeiro resultado é
Vamos guardar este resultado por hora! E resolver a integração por partes no segundo termo da equação (2). Vem comigo!
Passo 6
Temos a seguinte integral
Integrais que são polinômios vezes uma função trigonometria usualmente são convenientemente resolvidas integrando por partes. Se usarmos a regra do LIPTE (Logaritmo, Inversa, Polinomial, Trigonométrica e Exponencial) para escolhermos a prioridade da escolha de nosso , temos que
e
e também temos que
Se aplicarmos a seguinte fórmulinha para a integração por partes
Obtemos que
A integral restante pode ser identificada diretamente como uma integral conhecida, temos que
Substituindo este resultado na equação (4), temos que
Precisamos voltar com esse resultado dentro da equação (2)! Vamos fazer isso!
Passo 7
Utilizando a equação (5) e a equação (3) na equação (2) temos que
Podemos juntar alguns termos após expandir os produtos, para obter
Como temos que , podemos garantir que
Se substituirmos todos os resultados obtidos na equação (1), temos que
É a nossa série de Fourier! A questão é isso! Te vejo na próxima! Tchauzinho!