Encontre a série de Fourier em senos da função no intervalo ;
Esboce o gráfico da extensão de para a qual tal série converge.
Passo 1
Para encontrar uma série de Fourier em senos, buscamos a extensão ímpar da função . Assim, definimos:
Passo 2
Para calcular a série de Fourier, primeiro identificamos o período . Isto é, . Portanto, .
Assim, a série é dada por:
Novamente, a série aparece só em senos por que ela é uma função ímpar.
Passo 3
Vamos avaliar os coeficientes da série:
A integral do seno é fácil, mas a de nem tanto... Vamos usar integração por partes – duas vezes!
E, agora:
Portanto, combinando as fórmulas:
Passo 4
Vamos voltar de onde paramos...
Como e seno são ímpares, o produto é uma função par. Logo:
Tiramos a parcela com seno porque ela vai dar zero mesmo:
Passo 5
Uma forma alternativa é escrever :
Beleza, mas olha isso:
Passo 6
Assim, fica:
Passo 7
Para a função estendida, temos:
Mas a série de Fourier converge para , onde os pontos de continuidade são dados por:
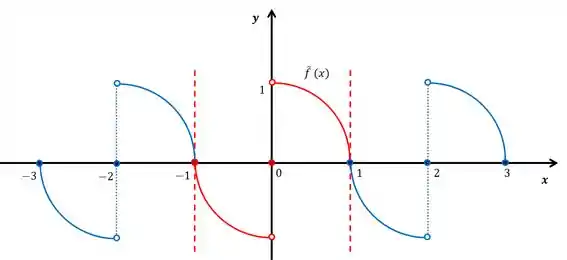
Assim, . A figura abaixo ilustra a função :
Resposta