Séries de Fourier, Séries de Fourier – funções pares e ímpares
Seja uma função - periódica, tal que se .
- Esboce o gráfico de no intervalo .
- Calcule a série de Fourier da função .
Passo 1
Letra a) Vamos fazer primeiro o gráfico. Bom, como o enunciado diz que a função é -periódica e nos dá o seu valor no intervalo , sabemos que esse é o período da função.
Vamos então desenhar . Não sabe fazer isso? Primeiro você tem que lembrar que o seno é como se fosse um “S” nessa parte perto da origem. Como fizemos abaixo em vermelho, ok?
Certo, mas queremos o módulo do seno, não o seno. Módulo significa “levar tudo para cima do eixo ”, grave isso. Como assim? A parte da direita já está acima do eixo , então não mexemos nela! A da esquerda, temos que levar para cima, espelhando:
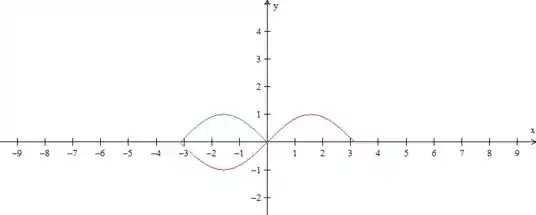
Certo, então a função é representada por esse dois morrinhos aí. Como esse é o período, agora temos que repetir o padrão:
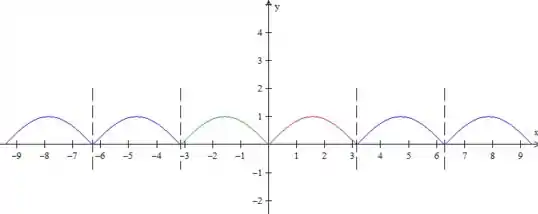
Pronto, essa é a função periódica . Percebeu que ela é uma função especial? Ela é espelhada no eixo , ou seja
Portanto, temos uma função par aqui.
Passo 2
Beleza, agora vamos montar o problema. Como a função é par, temos o seguinte:
Lembra que a função representada por Série de Fourier tem que ser periódica? Então, como o período da função é :
Passo 3
Agora vamos calcular .
Fazendo na expressão de e , temos:
Como em , temos:
Logo
Passo 4
Agora vamos calcular os outros ’s. Temos que:
O que nos dá
Beleza, agora temos que ver como integrar isso aqui né. Sempre que você encontrar uma integral de seno vezes um cosseno de números diferentes, pode pensar em aplicar as seguintes fórmulas trigonométricas:
O que nos dá:
Sem isso é meio complicado resolver a integral, então vale à pena memorizar essa fórmula aqui! A integral fica então:
Beleza, agora vamos analisar esses cossenos:
Para e
Para e
Para e
Percebeu então que esses cossenos são o mesmo que ? Vamos escrever isso
Se é ímpar isso aí dá zero, né? Temos isso aqui:
Não percebeu isso na hora? Deixa daquele jeito lá em cima mesmo! Não está errado, essa só é uma forma mais simplificada. Vamos lá então, tá quase acabando.
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Não podemos escrever direto no somatório porque isso só vale para par! Vamos definir então , porque isso garante que temos índices ímpares, ok? Para temos , que é onde a série começa, já que nos ’s ímpares são zero, portanto a nova série deve começar em . Temos então
Sendo:
Muito cuidado aqui, lembre-se sempre de dividir o por dois na hora da solução!