Considere a função
- Determine a série de Fourier de
- Se é a soma da série encontrada em a), esboce o gráfico de no intervalo , calcule e
Passo 1
a)
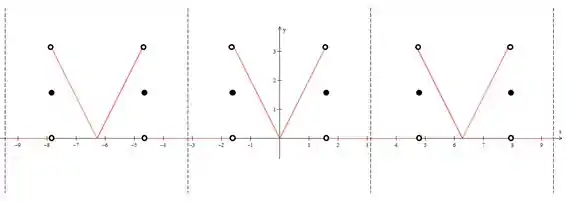
Vamos começar essa parada fazendo o gráfico dessa série de Fourier, mesmo que isso seja pedido no item b).
Repara que a nossa função está no intervalo de à , isso nos diz que o período dessa função vai ser .
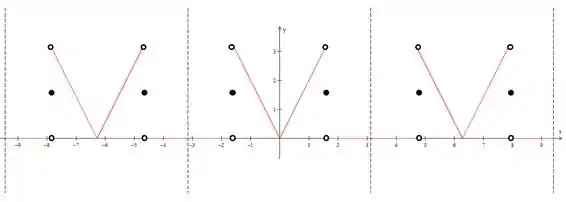
É bom sempre colocarmos essas retas tracejadas para delimitar os períodos para entendermos bem essa paradinha.
Repare nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de descontinuidade a função vai vale a média dos limites laterais. Neste caso
E
Esse gráfico ajudou a vermos como fica a parada, a grande questão agora é fazer os termos dessa série.
Passo 2
Beleza, agora vamos montar o problema. Ele quer a série de Fourier dessa função. Então precisamos fazer
Com
Como já vimos o período é , então
Passo 3
Vamos começar fazendo
Substituindo
Substituindo o valor de temos uma integral só naquela parte onde não é
Separando esse módulo
Passo 4
Vamos agora para
Substituindo o valor de temos uma integral só naquela parte onde não é
Separando esse módulo
Vamos resolver essa integral separada
Passo 5
A nossa integral é
Vamos resolver essa integral por partes
Vamos ter
Assim vamos ter
Passo 6
Voltando para
Passo 7
Vamos agora achar , mas veja que a função é par, logo podemos escrever que:
Passo 8
A nossa série de Fourier vai ser
Substituindo os valores dos coeficientes vão ser
Passo 9
b)
Primeiro vamos relembrar como é o gráfico dessa parada
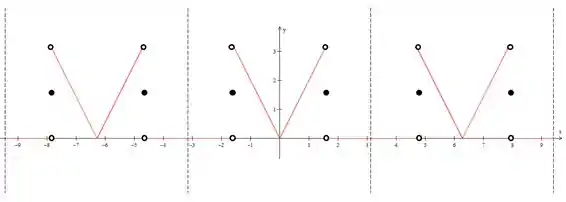
Queremos achar o valor da soma em e . Primeiro vamos lembrar que a soma vai ser
Temos que ver a que valor entre e . Vamos começar com
Queremos essa parada entre e , temos ali , que é , ou seja,
Os nossos intervalos do período vão ser sempre
Ou seja, entre ímpares de , como é entre e , vamos ter
Para voltarmos para temos que subtrair todo mundo em , fazendo isso vamos ter
Isso vai ficar
Ou seja,
Esse ponto por acaso é um ponto de desigualdade, então
Assim temos a soma onde queremos
Passo 10
Vamos agora fazer a mesma coisa para
Temos que ver a que valor entre e . Já vimos a lógica para passar para esse intervalo, então vamos começar dividindo
Então
Para chegarmos no temos que fazer uma subtração de todo mundo com
Isso vai ficar
Ou seja,
Esse ponto não é o de desigualdade, então, temos que olhar na função onde ele se encaixa. A função é
E é igual a , ou seja, esse valor está entre e , assim
Assim temos a soma onde queremos
Resposta
a)
b)