Seja a função definida por
- Determine a série de Fourier em senos de
- Esboce o gráfico da série de Fourier obtida no item (a) no intervalo
- Calcule o valor da série
Passo 1
OK, vamos começar com a letra (a). Temos uma função definida no intervalo e o problema nos pediu a série de Fourier em senos de . Assim, precisamos da extensão ímpar desta função, que vamos chamar de . Vamos ver a expressão dessa função com mais calma daqui a pouco.
Ok, então vamos calcular o coeficiente associado à série em senos de . Pela fórmula geral:
Como a nossa função está definida em , a extensão vai considerar o intervalo espalhado e será -periódica. A fórmula geral se refere às funções -periódicas, então vamos ter no nosso caso:
Como a função é ímpar e a função seno também é ímpar, o integrando será uma função par e teremos:
A extensão tem a mesma expressão de no intervalo , assim:
E vamos ter que usar integral por partes para resolver esse problema. Pela regra do LIATE, teremos:
Derivando:
O é o que sobra no integrando:
Boa, assim vamos ter:
Parece que não mudou muita coisa, mas vamos aplicar novamente a integral por partes na outra integral:
Abrindo:
Apareceu novamente a integral do início. Então vamos chamar
E ir substituindo:
E vamos isolar :
Assim, vamos ficar com:
Ou para ficar do jeitinho que a questão pediu:
Legal, então a série associada é:
Passo 2
Agora vamos para letra (b). Agora que precisamos esboçar o gráfico da série de Fourier, vamos olhar melhor para a nossa extensão ímpar que usamos. Em o gráfico será o mesmo de dado
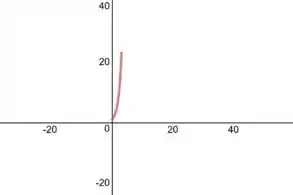
Show, então definimos a função para o intervalo espalhado . Para que seja ímpar, a expressão neste intervalo tem que ser:
Portanto, vamos ter:
Adicionamos ao esboço também:
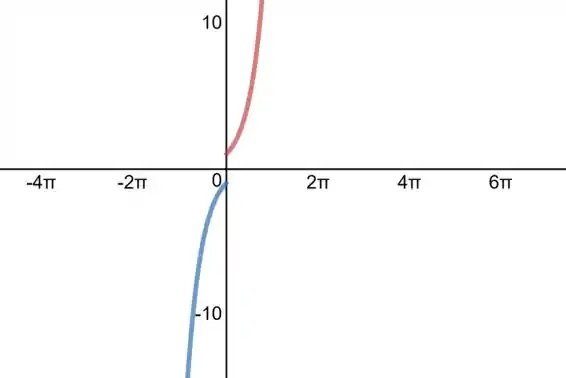
Como definimos para o intervalo , a extensão será -periódica:
Assim, repetimos para completar o intervalo :
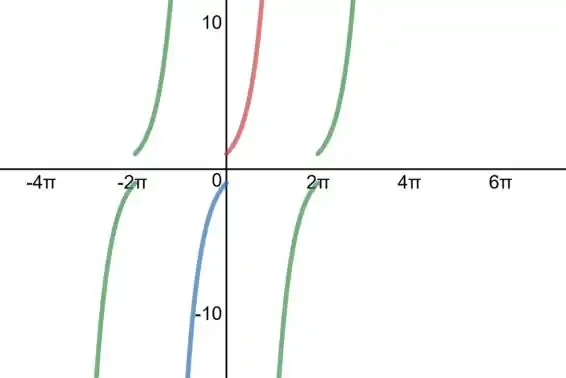
Para fechar, completamos os pontos que faltam. A série de Fourier vai ter o gráfico igual ao da extensão para todos os pontos em que a extensão é contínua. Então tudo certo até agora. Já nos pontos de descontinuidade, que estão justamente nas fronteiras das expressões, a série de Fourier converge para o valor médio das expressões. Assim, temos:
Assim, marcamos esses pontos (também já considerando que é periódica para repetir):
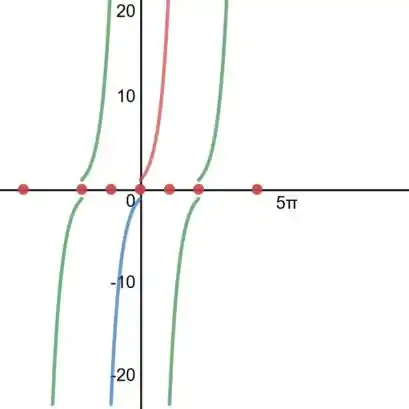
Passo 3
Show, agora vamos para letra (c). Precisamos calcular o valor da série:
A ideia aqui é relacionar a série que encontramos na letra (a) com esta ali para encontramos o valor a partir da função dada. Legal, temos isso aqui:
Para tirar esse seno, podemos pegar . Assim, teremos:
Vamos olhar para o nosso amiguinho seno:
Sempre que for um número par, será divisível por , então teremos que:
Assim, só sobrarão os termos ímpares. Para escrevermos mudamos o índice para . E teremos:
Novamente voltamos para ele:
Separando, temos:
E assim:
Pela expressão, temos:
Assim, vamos ter:
E é isso. 😊
Resposta
(a)
(b) 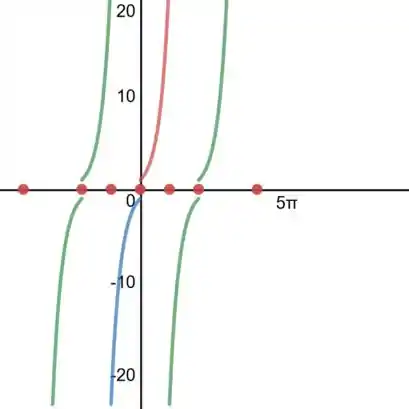
(c)