Séries de Fourier – funções pares e ímpares
Seja uma função de período tal que para todo .
- Sabendo que é uma função ímpar, determine a expressão de no intervalo .
- Determine a série de Fourier da função .
- Usando o item (b), calcule a soma da série numérica . Justifique sua resposta.
Passo 1
Letra a)
Vamos fazer um desenho dessa expansão de , ok?
Essa é a definição de que o problema deu de a :
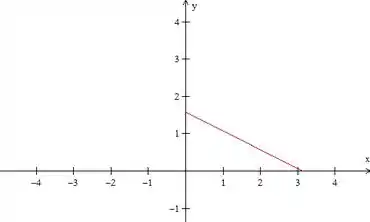
Vamos fazer a extensão ímpar dessa função, porque o problema pede uma série de senos. Primeiro nós espelhamos ela em relação ao eixo
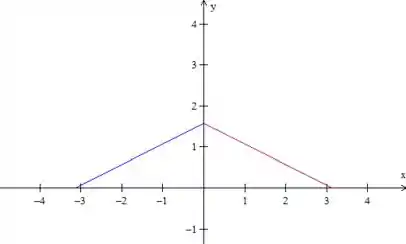
Espelhamos essa reta azul no eixo :
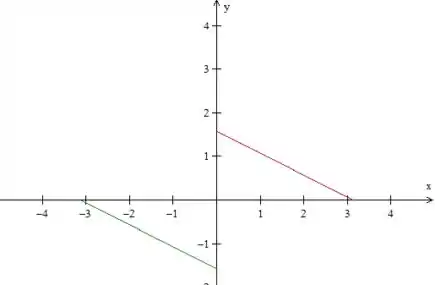
O período de é então essa parte verde mais a vermelha, para termos uma função em série de senos temos que ter ímpar como já vimos, para isso devemos pegar a função entre e , fazendo essa marotagem que fizemos ali de espelhar no eixo e depois no eixo , isso garante que nossa função seja ímpar, mas para isso tudo dar certo temos que pegar de à fazendo o período ser
Passo 2
Tá, mas o que o problema pede é a expressão de para . Nós sabemos que
para todo .
Como a função é ímpar, sabemos que
Logo, a expressão de para o intervalo que o problema quer é dada por:
Passo 3
Letra b)
Beleza, agora vamos montar o problema. Como a função é ímpar, temos o seguinte:
Como o período da função é , temos:
Passo 4
Vamos calcular os ’s. Temos que:
Agora vamos substituir a expressão de :
Agora vamos fazer a integração por partes:
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Passo 6
Letra c)
Como é seccinalmente contínua, temos que
Em todo ponto de continuidade de . E, como é contínua em , temos: