Questão 1: Seja a função
b) Esboce o gráfico da série de Fourier obtida no item no intervalo .
Passo 1
Bem, aqui basta nós desenharmos a extensão par de e periódica de :
A extensão tem a seguinte definição:
E
Isso significa que a nossa função é periódica de período , tá ligado? Agora a gente pode desenhar!
Passo 2
Primeiro a gente vai desenhar o seno de :
Para isso, vamos encontrar alguns pontos que nos auxilie:
Então:
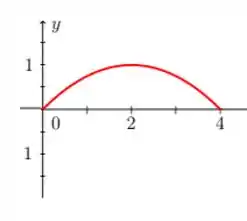
Para a extensão par, , basta fazer uma simetria com relação ao eixo :
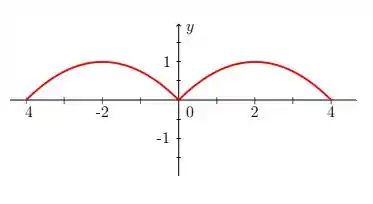
Agora basta repetir esse padrão de :
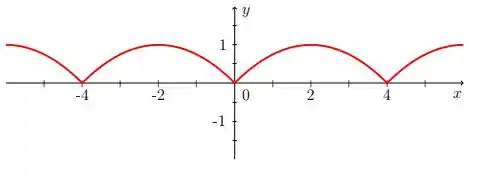
Resposta
Exercícios de Livros Relacionados
(a) Sejam v 1 ,v 2 e v 3 três vetores ortogonais dois a dois em três dimensões, e seja u qualquer vetor tridimensional. Mostre que u = a 1 v 1 + a 2 v 2 + a 3 v 3 , Em que a i = u ∙ v i v i ∙ v i , i
f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função
Considere a função f definida no problema 21, e seja e m = f x - s m ( x ) . f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Faça o gráfico de e m ( x ) em função de x para 0 ≤ x ≤ 2 para diversos valores
f x = x ,- 1 ≤ x1 f x + 2 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função de
Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. x 2