Seja:
- Esboce o gráfico da extensão ímpar e periódica de período de . Defina a função nos pontos de descontinuidade de forma que sua série de Fourier convirja para esse valor
- Calcule a série de Fourier da extensão ímpar de determinada no item
Passo 1
Falai galera, vamos começar? Então, olha, uma função ímpar é uma função que tem sempre:
Em grafiquês, é como se a função fosse espelhada em relação ao eixo e depois em relação ao eixo (ou vice-versa). Pegando então nosso :
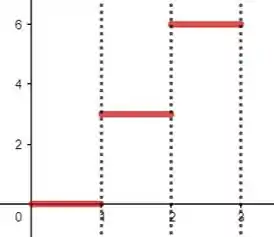
Podemos espelhar ele pra achar a extensão ímpar:
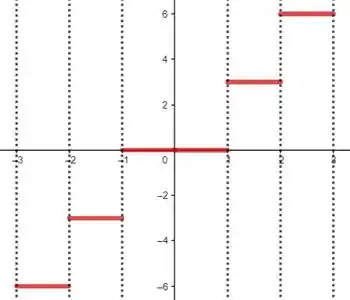
E a lei de formação dessa função espelhada é:
Vemos que essa extensão tem um problema. Na verdade, tem problemas, que são os pontos de descontinuidade. Podemos usar o Teorema da Convergência de Fourier que diz que nos pontos de descontinuidade a Série de Fourier converge para:
Como os pontos de descontinuidade são . Fazemos, pra esses pontos, nessa ordem:
Logo o gráfico fica:
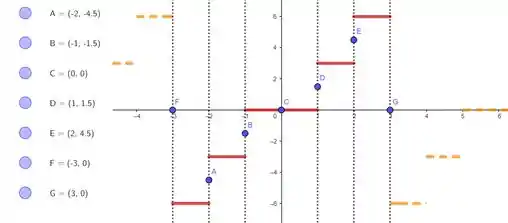
E a função:
Passo 2
A série de Fourier galera, vai ter essa cara aqui:
Onde é o período da função. Nesse caso, vamos ter e logo . Temos uma facilidade na nossa vida aqui, no entanto! Como nossa é uma função ímpar, não vamos precisar calcular termos de ! Afinal:
E toda integral de função impar do tipo:
Nossa série de Fourier fica mais simples:
E ainda dá pra simplificar mais ainda. Afinal, como seno é uma função ímpar, temos:
E portanto, como vale:
Temos:
Vamos continuar daí em diante no próximo passo, ok?
Passo 3
Show! Vamos lá! Primeira coisa a fazer é achar . Lembra lá do enunciado que tínhamos:
Lembrou? Portanto fica:
Duas integrais da mesma coisa mas com limites de integração diferentes. Bem, de forma indefinida, temos:
Aplicando os limites de integração, temos então:
Fazendo a distributiva das constantes e juntando o termo em comum:
O que resulta finalmente em:
Olha, aqui praticamente acabou viu? Vamos só tentar simplificar isso!
Passo 4
Show, nota o seguinte. Indo de até , vemos que:
Se formos continuar vendo isso pra mais , chegaremos a conclusão que:
Portanto, podemos separar em partes também, já que:
Vamos ter:
Separando a série de Fourier em termos pares e ímpares, temos:
E se adicionarmos a restrição no somatório direita
Basta substituir os valores não nulos de , onde com aquelas restrições é o para termos pares não múltiplos de e é o valor de para valores de ímpares:
Aeee, acabaaamos!
Resposta
OBS: o texto significa, resumidamente, que não pode ser um múltiplo de