Encontre a série de Fourier para a função dada e esboce o gráfico da função para a qual a série converge em um intervalo de três períodos.
Série de senos, período .
Passo 1
Vamos começar fazendo o gráfico, para a gente poder visualizar melhor a questão, ok? Primeiro, vamos desenhar os dados do enunciado:
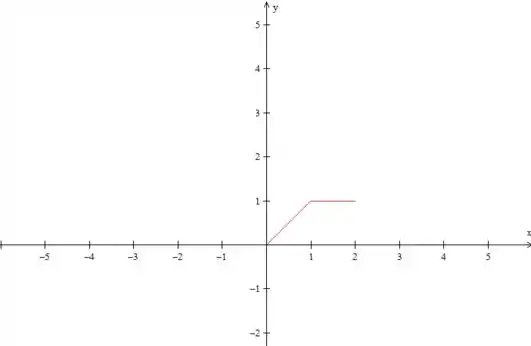
Até aqui nada demais, né? Como a questão pede uma série de senos, temos que fazer uma extensão ímpar dessa função. Então, o próximo passo é espelhar isso que desenhamos do eixo , dessa forma:
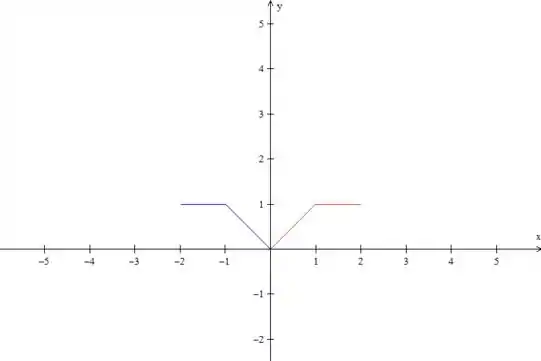
Mas isso seria uma extensão par, não é? Pra fazermos uma extensão ímpar temos que rebater essa parte azul no eixo , ou seja, jogar ela para baixo:
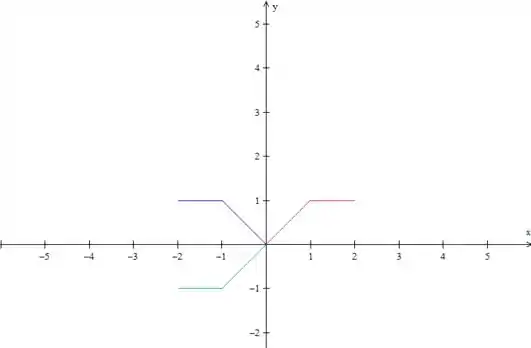
Certo, o período da função que queremos é então essa parte verde mais a vermelha! Como esse é o padrão que se repete, vamos copiá-lo, tanto para a esquerda como para a direita, olha só:
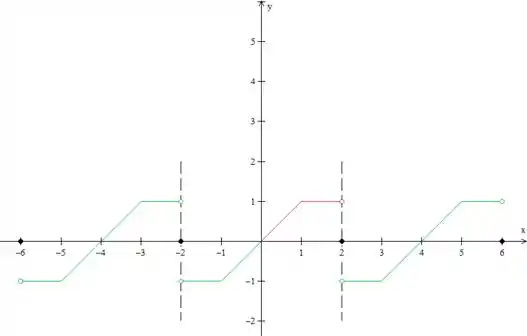
Pronto, temos então três períodos da função, como pede o enunciado. É bom você sempre desenhar esse tracejado grande para marcar o período da função, para não se perder!
Repare nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de salto, a função vale a média dos limites laterais. Nesse caso:
Nós colocamos então as bolinhas cheias em repare que todas as retas tem bolinhas vazias nas suas extremidades). Não poderia ser diferente, né? Uma extensão periódica ímpar sempre apresenta:
Como a gente já viu.
Passo 2
Beleza, agora vamos montar o problema. Como a função é ímpar, temos o seguinte:
Como o período da função é como o enunciado pediu, temos:
Passo 3
Vamos calcular os ’s. Temos que:
Como temos mais de uma expressão para em , precisamos dividir essa integral em duas:
Agora vamos fazer a integração por partes:
Como essa expressão é um pouco complexa (já que envolve seno e cosseno), não vamos fazer aquela análise para ’s pares e ímpares ok? Vamos deixar assim mesmo.
Passo 4
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá