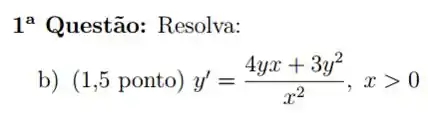
Passo 1
Quando a EDO está nesse formato é interessante vermos se ela é homogênea, então vamos calcular .
Então a equação é homogênea e devemos fazer a seguinte substituição:
e
Passo 2
Substituindo na equação:
Agora temos uma equação separável, vamos resolvê-la:
Integrando dos dois lados:
Devemos resolver o lado esquerdo por fracoes parciais, então expandindo temos:
Então:
Substituindo :
Resposta
Exercícios de Livros Relacionados
Nos problemas 11-30, resolva a equação diferencial dada usando uma substituição apropriada. d y d x = y x + x 2 y 2 + 1
Nos problemas 11-30, resolva a equação diferencial dada usando uma substituição apropriada. x 2 + x y - y 2 d x + x yd y = 0
Nos problemas 11-30, resolva a equação diferencial dada usando uma substituição apropriada. xd x + ( y - 2 x )d y = 0
Nos problemas 31-44, resolva a equação diferencial dada sujeita à condição inicial indicada. y 2 + 3 x y d x = 4 x 2 + x y d y ; y 1 = 1
Nos problemas 11-30, resolva a equação diferencial dada usando uma substituição apropriada. x d y d x - y = x 2 + y 2