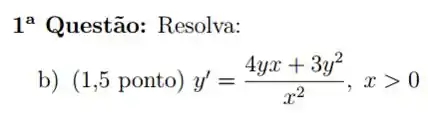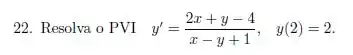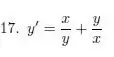Exercícios de EDO Homogênea - Lista de Exercícios Resolvida
Questão 2
Determine se a função dada é homogênea. Especifique o grau de homogeneidade se for o caso.
Ver solução completaQuestão 6
Considere a equação da forma
Onde , , , , , são constantes reais.
- Quando , pode-se reduzir essa equação em uma equação homogênea nas variáveis e se e , onde e são soluções do sistema linear.
- Quando e e não simultaneamente nulos, pode-se reduzir essa equação em uma equação de variáveis separáveis nas variáveis e , se fizermos a substituiç��o
- Quando e e não simultaneamente nulos, pode-se reduzir essa equação em uma equação de variáveis separáveis nas variáveis e , se fizermos a substituição
Questão 7
Dada a equação
a)Mostre que essa equação diferencial é homogênea e diga qual a substituição que pode ser utilizada para torná-la separável.
b)Resolva a equação
Ver solução completaQuestão 9
Nos exercícios 19 a 21 use o método desenvolvido na questão 18, para determinar a solução geral das equações.
![]()
Questão 10
Nos exercícios 19 a 21 use o método desenvolvido na questão 18, para determinar a solução geral das equações.
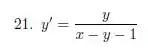
Questão 13
Resolva as seguintes equações diferenciais, e problemas de valor inicial.
Ver solução completaQuestão 14
Resolva as seguintes equações diferenciais ou problemas de valor inicial, conforme seja o caso.
c)
Ver solução completaQuestão 15
Determine as soluções gerais, explicitas ou implícitas, das equações diferenciais de 1ª ordem acima, com métodos apropriados para cada caso.
Ver solução completaQuestão 18
Questão 1: Resolva as seguintes equações diferenciais ou problemas de valor inicial, conforme seja o caso.
Ver solução completaQuestão 22
Determine a solução geral da equação que satisfaz a condição inicial de
Ver solução completaQuestão 24
Mostre que, se e são constantes positivas e se é qualquer número real, então toda
solução da equação
tem a propriedade que quando então . Sugestão, analise os casos onde separadamente.
Ver solução completaQuestão 25
Resolve as seguintes equações diferenciais. No caso da letra a), resolve o problema de valor inicial associado.
Questão 31
Mostre que a seguinte equação é homogênea e resolva-a com a substituição :
Ver solução completaQuestão 34
Dadas as funções, determine quais são homogêneas.
I-
II-
III-
( ) Todas são homogêneas
( ) Todas não são homogêneas
( ) Apenas a II
( ) Apenas a I
( ) Apenas a III
Ver solução completaQuestão 35
Questão 1: Resolva as seguintes equações diferenciais ou problemas de valor inicial, conforme seja o caso.
Ver solução completaQuestão 37
Resolva a seguinte equação diferencial ou problema de valor inicial conforme seja o caso:
(c)
Ver solução completaQuestão 39
Um tanque de 120 litros de água contem 10kg de sal. Você o irriga com água limpa a uma taxa de 2 litros por minuto e deixa a mistura escoar com a mesma vazão. Encontre uma fórmula que expressa a quantidade de sal (em kilos) no tempo t (em minutos).
Ver solução completaQuestão 41
Uma massa de 9kg desloca de 0,1m para baixo uma mola. Deslocamos a massa de 1 m para baixo e soltamos. Encontre a função que descreve a posição da massa em função do tempo. Use que a aceleração da gravidade é
Ver solução completa