PUCRIO – Física 2 – 2020.1 – G2 – M. Escolha
. Um fio muito longo é feito juntando-se outros dois fios com densidades lineares diferentes e a junção dos fios pode ser localizada no ponto . A figura abaixo mostra uma porção do fio, centrada na junção. O fio é esticado sob uma tensão . No instante , é produzido um pequeno pulso transversal, localizado no ponto . Considere as distâncias indicadas na figura abaixo. Em que instante de tempo o pulso atinge o ponto ?
.
.
.
.
.
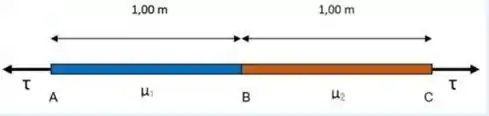
Passo 1
Vamos juntos lidar com esse problema!
Temos um caso de pulso em uma corda sofrendo tração e onde uma metade tem uma certa densidade linear e a outra metade uma densidade diferente.
Para achar quanto tempo o pulso leva para ir de até , temos que saber a velocidade da onda na corda, então vamos usar a expressão que nos fornece essa velocidade, dada por:
Como podemos ver a velocidade depende da densidade linear, logo teremos velocidades diferentes em cada metade da corda.
Achando essas velocidades basta usar uma relação da cinemática que já é velha conhecida nossa.
Mãos à obra então!
Passo 2
Vamos encontrar a velocidade da parte azul da corda, onde temos .
Temos que notar que a tensão é dada em newtons, logo essa densidade deve ser em , assim temos que:
Então:
Com isso o tempo que a onda leva para passar pela parte azul é:
Passo 3
Vamos agora ver a velocidade da parte laranja, temos que , passando para , temos:
Então:
Com isso o tempo que a onda leva para passar pela parte azul é:
Passo 4
Então o tempo total para a onda atravessar a corda é:
Logo a alternativa correta é a letra .
Resposta
.