Uma onda progressiva transversal está se propagando numa corda infinita esticada. Escolhemos como eixo Ox a extensão da corda quando em repouso e o sentido da progressão como positivo. Seja Oy a direção da vibração da corda. São dadas a velocidade de propagação da onda, , e a densidade linear de massa da corda, . No instante , a forma da onda é dada por , onde , .
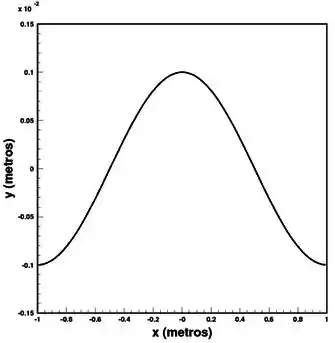
(a) Determine o comprimento de onda dessa onda e faça um esboço dessa onda para em , indicando as escalas escolhidas no eixo Ox e no eixo Oy.
(b) Determine o período T dessa onda e ache a expressão matemática do deslocamento transversal da corda em função de (x,t).
(c) Determine a magnitude da tensão F na corda.
(d) Calcule a partir da potência instantânea (em Watts) a potência média, em um período, transportada pela onda.
Passo 1
(a) O comprimento de onda está relacionado com o número de onda:
Temos que a equação dessa onda é
Temos que esboçar o intervalo
Juntando essas informações, chegamos no seguinte gráfico:
Passo 2
(b) O período dessa onda está relacionado com a velocidade e o comprimento de onda:
Queremos a equação do deslocamento transversal da onda em função de (x,t). De modo geral temos:
Como a onda se propaga no sentido positivo de x, vamos usar . E vamos usar .
Juntando os dados:
Passo 3
(c) Queremos a tensão (F) na corda. Para uma onda se propagando na corda temos a seguinte relação:
Onde
Passo 4
(d) Primeiro vamos calcular a potência instantânea transportada por essa onda.
Ela vai ser a componente transversal da tensão na corda () vezes a velocidade transversal na corda ()
Juntando tudo:
Passo 5
Para a potência média em um período, usamos o teorema do valor médio
O segundo termo é justamente o valor médio de seno ao quadrado. Como este varia harmonicamente entre 0 e 1, em um período completo temos que:
Então:
Resposta
- ,
- ,