Uma onda transversal senoidal se propaga em uma corda no sentido negativo do eixo . A Figura abaixo mostra o deslocamento em função da posição no instante . A tensão na corda é e a massa específica linear . Assuma que a onda é da forma .
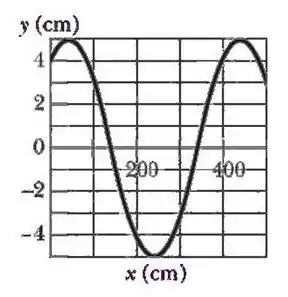
Determine a amplitude.
Encontre a velocidade da onda e a frequência da onda.
Calcule a taxa média de transporte de energia.
Passo 1
Analisando o gráfico, podemos ver que a distância do eixo até um ponto de máximo, ou seja, a amplitude é:
Passo 2
Para determinar a velocidade, podemos usar a seguinte relação:
Substituindo os valores, temos:
Perceba que tivemos que passar a densidade linear para o S.I!
Para calcular a frequência, podemos usar a seguinte relação:
Do gráfico, . Então:
Novamente tivemos que passar para o S.I! Fique esperto!
Passo 3
A potencia média, taxa média de transporte de energia, é dada por:
Onde é a amplitude, substituindo os valores, temos:
Resposta
.
;