Exercícios Resolvidos de Velocidade e Potência de uma Onda na Corda

Ver Teoria

Exercício 27 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59

Enunciado

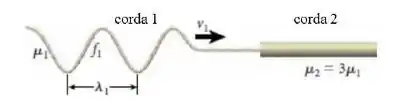
Como mostrado na figura, uma onda senoidal se propaga para a direita com velocidade v1 ao longo da corda 1, que tem uma densidade linear de massa μ1. Esta onda tem uma frequência f1 e um comprimento de onda λ1. Como a corda 1 está presa à corda 2 (que tem densidade linear de massa μ2= 3μ1), a primeira onda excitará uma nova onda na corda 2, que também se propaga para a direita. Qual é a velocidade v2 da onda produzida na corda 2?

a) ;

b) ;

c) ;

d);

e) ;

Passo 1

Vamos lembrar a fórmula que relaciona a tensão, densidade linear da corda e a velocidade:

Repara ali que eu não coloquei o índica 1 na tensão.Para e pensa: POR QUEEEEEE?

Porque a tensão na corda mais pesada vai ser igual na corda mais leve. Na hora que o pulso passa de uma corda pra outra, a tensão é transmitida. Show? Rearranjando então:

Para a corda mais pesada:

Igualando os dois:

Resposta

Letra A.

Exercícios de Livros Relacionados

A figura mostra o deslocamento y do ponto de uma corda situado em x = 0 em função do tempot quando uma onda passa pelo ponto. A escala do eixo y é definida por y=6,0m m . A onda tem a forma y x ,t = y

Em um experimento com ondas estacionárias, uma corda de 90c m de comprimento está presa a um dos braços de um diapasão excitado eletricamente, que oscila perpendicuJarmente à corda com uma frequência

Uma onda senoidal transversal se propaga em corda no sentido positivo de um eixo x com uma velocidade de 80m / s . No instante t = 0 , uma partícula da corda situada em x = 0 possui um deslocamento tr

Na figura a , a corda 1 tem uma massa específica linear de 3,00g / m e a corda 2 tem uma massa específica linear de 5,00g / m . As cordas estão submetidas à tensão produzida por um bloco suspenso de m

A figura mostra a velocidade transversal u em função do tempo t para o ponto de uma corda situado em x = 0 , quando uma onda passa por ele. A escala do eixo vertical é definida por u s = 4,0m / s . A