Uma corda uniforme de massa e comprimento está pendurada em um teto.
Mostre que a velocidade de uma onda transversal na corda é função de, a distância da extremidade inferior, e é dada por
Passo 1
Na primeira situação temos a seguinte figura:
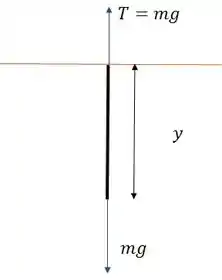
Pela condição de equilíbrio, a tensão na corda vale .
E a densidade linear vale .
Aplicando a fórmula:
Como queríamos demonstrar! :)
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A figura mostra o deslocamento y do ponto de uma corda situado em x = 0 em função do tempot quando uma onda passa pelo ponto. A escala do eixo y é definida por y=6,0m m . A onda tem a forma y x ,t = y
Em um experimento com ondas estacionárias, uma corda de 90c m de comprimento está presa a um dos braços de um diapasão excitado eletricamente, que oscila perpendicuJarmente à corda com uma frequência
Uma onda senoidal transversal se propaga em corda no sentido positivo de um eixo x com uma velocidade de 80m / s . No instante t = 0 , uma partícula da corda situada em x = 0 possui um deslocamento tr
Na figura a , a corda 1 tem uma massa específica linear de 3,00g / m e a corda 2 tem uma massa específica linear de 5,00g / m . As cordas estão submetidas à tensão produzida por um bloco suspenso de m
A figura mostra a velocidade transversal u em função do tempo t para o ponto de uma corda situado em x = 0 , quando uma onda passa por ele. A escala do eixo vertical é definida por u s = 4,0m / s . A