Uma corda de massa m e comprimento L está suspensa verticalmente com um corpo de massa M preso na extremidade inferior da corda.
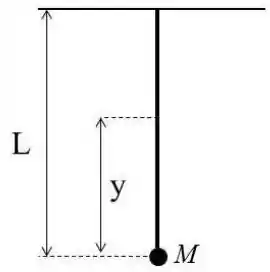
a) Calcule a velocidade de uma onda transversal na corda em função de y, a distância da extremidade inferior.
b) Calcule o tempo para uma onda transversal percorrer o comprimento da corda.
Passo 1
a) A velocidade de uma onda na corda é dada por
Onde T é a tração na corda e é a densidade linear,
Passo 2
Repare que podemos dizer que a massa total da corda é
Mas se quisermos saber a massa só de um pedaço da corda? Digamos que é a massa de um pedaço de comprimento da corda. Como é constante, então
A tração na corda vai ser a soma dos pesos. Só que cada parte da corda vai ter uma tração diferente.
Pense que quando , tração tem que compensar só o peso da massa M, mas quando , tem que compensar o peso da massa M mais o peso da corda inteira.
Por isso, podemos dizer que
Se jogarmos na equação da velocidade:
Como
Passo 3
b) Calcular o tempo que a onda demora para percorrer o comprimento da corda (L).
Temos que lembrar que
Como queremos t, podemos reescrever
Integrando entre e :
Substituindo
Botando um monte de coisa em evidência pra ficar bonitinho: