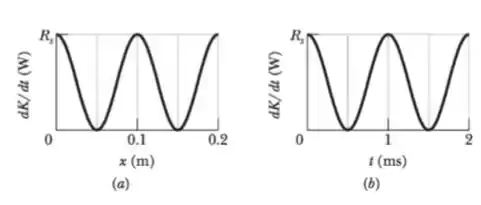
Uma onda senoidal é produzida em uma corda comum a densidade linear . Enquanto a onda se propaga, a energia cinética dos elementos de massa ao longo da corda varia. A Figura abaixo mostra, em um certo instante, a taxa de energia cinética em função da distância ao longo da corda. A Figura abaixo é semelhante, exceto pelo fato de que esta mostra a taxa em função do tempo para um dado elemento de massa situado em um certo ponto. Nos dois casos, a escala do eixo vertical é definida por . Qual é a amplitude da onda expressa em metros?
Passo 1
Bem , precisamos lembrar um conceito não tão comum para resolvermos esse exercício.
Precisamos lembrar que a potência média pode ser calculada como derivada da energia cinética. Isso tudo porque a potência é a derivada do trabalho
Pelo teorema do trabalho, onde relacionamos o trabalho com a energia cinética, podemos dizer que
E agora faz sentido o exercício, pois conseguimos através de uma fórmula relacionar a potência com a amplitude . Pela fórmula:
Onde é a densidade linear da corda que foi dada pelo enunciado, é a velocidade de propagação da onda que é dada por
Onde é o comprimento de onda que conseguimos encontrar pelo gráfico e é a frequência que também conseguimos encontrar pelo gráfico.
Isolando a amplitude
Passo 2
Vamos encontrar os dados que nos falta para resolver o exercício, a potência média foi dada, pois no enunciado o problema fala que . Vamos analisar o ponto em e .
Então
Passo 3
O comprimento de onda iremos descobrir analisando o gráfico por e a frequência pelo gráfico por .
Se pensarmos numa onda senoidal
Temos que a sua velocidade transversal é dada por
E pensarmos num pedaço da corda com essa velocidade e massa a sua energia cinética vai ser
A variação da energia cinética com o tempo vai ser dada por
Usando arco duplo
Finalmente chegamos em
Ou seja, um gráfico de vai oscilar no tempo e no espaço o dobro o que oscila um gráfico .
Olhando o gráfico de por , vemos que o comprimento de onda pra essa oscilação é . Como oscila mais devagar, então o comprimento de onda pra vai ser o dobro disso, ou seja,
Já o gráfico por , o período dessa oscilação é . Como oscila mais devagar, então o período pra é o dobro disso, ou seja,
Como queremos a frequência basta usar
Passo 4
Já encontramos todos os dados para calcular a amplitude da onda, assim
Beleza, encontramos a amplitude!
Resposta
Alternativa