UFF – Física III – P2 – 2022.1 – Q7
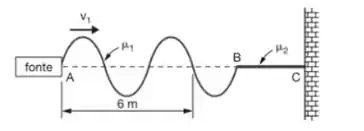
Uma fonte vibratória produz uma onda transversal periódica, que se propaga com velocidade , numa corda AB, cuja densidade linear de massa é , conforme mostra a figura. Essa corda está ligada a uma outra, BC, cuja densidade linear de massa é . Para a onda que se propaga na corda BC, qual é seu comprimento de onda?
Passo 1
E aí, galerinha! Tudo na paz por aí?
Nessa questão vamos precisar lembrar de alguns conceitos como por exemplo, que na refração a frequência da onda permanece constante, que pela equação fundamental da ondulatória:
Note que no problema é pedido pra gente calcular ... então como resolver esse problema aí?
VEM COMIGOOO!!!!
Passo 2
Da figura dada, temos:
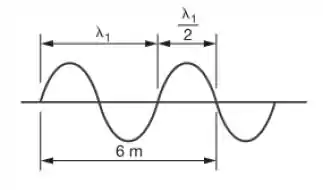
Ou seja, conseguimos a partir desse equacionamento concluir que:
Pronto, uma das variáveis já conseguimos! Agora faltam as outras!
Passo 3
Das equações de ondas também tem-se as seguintes igualdades:
Note que T é a tensão que a corda é submetida e os são as densidades lineares.
Como as cordas são submetidas à mesma tensão, temos que , portanto da equação do passos 1, temos:
O enunciado nos deu as densidades lineares e iguais a e , respectivamente. Agora é só a gente substituir na equação e tcharammmm!!!
Encontramos nosso comprimento de ondaaaaa!!!