Uma onda senoidal monocromática se propaga em um trecho de uma corda em que essa é uniforme. A corda, disposta horizontalmente, apresenta, no entanto, um segundo trecho em que a sua densidade linear é uniforme, mas diferente da inicial. A tensão na corda é a mesma ao longo dela toda. As figuras a seguir representam fotografias da corda no primeiro trecho (superior) e no segundo trecho (inferior).
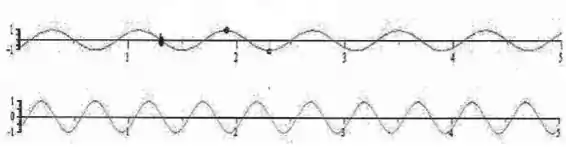
As figuras foram construídas com escalas verticais distintas e muito exageradas, mas com a mesma escala horizontal. Justifique cada resposta.
A frequência de onda é a mesma nos dois trechos?
O comprimento de onda é o mesmo nos dois trechos?
Qual trecho apresenta densidade linear maior?
Indique na figura a direção e o sentido da velocidade instantânea do ponto material da corda indicado na figura. Indique também um ponto cuja velocidade instantânea seja igual a zero
Passo 1
A frequência da onda é dada pela fonte que gera a onda. Essa fonte que vai determinar a frequência com que a onda vai se propagar.
Então não importa a característica do trecho a frequência é igual. Por isso a resposta é: Sim!
Passo 2
O eixo do gráfico é tempo ou distância ? Distância, pois o enunciado diz que é uma fotografia da onda, então fixou um tempo e a foto mostra a posição da corda em cada distância .
Se o eixo é distância então fica fácil descobrir o comprimento de onda. Basta olharmos a distância em que a onda começa a se repetir.
Fazendo isso vemos que no trecho a onda começa a se repetir ente e 1, já a onda no trecho começa a se repetir pouco antes de .
E isso mostra que o comprimento de onda no trecho é maior que no trecho .
Passo 3
Qual trecho tem maior densidade linear? Bem, a única formula que temos que relaciona densidade linear é a da velocidade, certo?
Mas não temos a velocidade, então não conseguimos usar essa fórmula ainda. Mas sabemos que a velocidade pode ser dada por:
A frequência já vimos que é a mesma nos dois trechos, já o comprimento de onda vimos que um é maior que o outro. Podemos relacionar isso com o comprimento de onda, já que a tensão também é a mesma para toda a corda.
Como e são constantes para os dois trechos da corda. Temos a seguinte equação par cada trecho.
Dividindo uma pela outra temos:
No item anterior vimos que , então a igualdade que temos acima, mostra que:
Passo 4
Vamos começar do mais simples, os pontos onde temos a máxima amplitude e a mínima, são pontos em que a velocidade é zero. Então vamos indica-los de vermelho
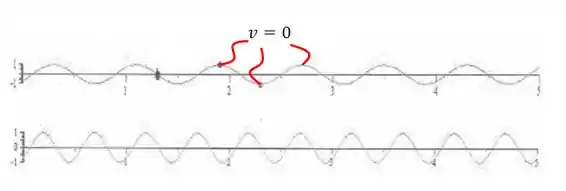
E agora vem a parte que temos que analisar o movimento da partícula quando o tempo passar. Se a velocidade da onda for positiva, adotando o sentido positivo para a direita. Então a partícula vai subir quando o tempo passar, pois a amplitude do ponto anterior ao analisado é maior que a do ponto pedido, onde .
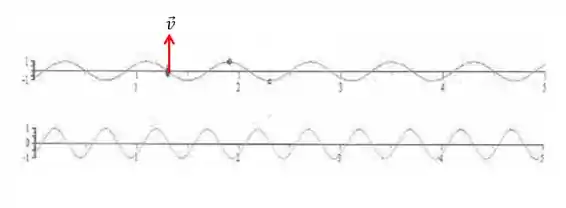
Resposta
Sim.
Não,