O gráfico representa, num dado instante, a velocidade transversal dos pontos de uma corda, na qual se propaga uma onda senoidal na direção positiva do eixo dos .
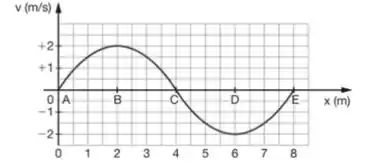
A velocidade de propagação da onda é de 24 m/s. Sejam A, B, C, D e E pontos da corda. Considere, para o instante representado, as seguintes afirmações:
A frequência da onda é
Os pontos A, C e E têm máxima aceleração transversal (em módulo)
Os pontos A, C e E têm máximo deslocamento transversal (em módulo)
Todos os pontos da corda se deslocam com velocidade de 24 m/s na direção do eixo .
Estão corretas:
- Todas
- Somente IV
- Somente II e III
- Somente I e II
- Somente II, III e IV
Passo 1
E aí, galerinha! Tudo na paz por aí?
Nessa questão a gente vai entender alternativa por alternativa o porquê dela está falsa ou verdadeira!
Passo 2
I – Incorreta. Note que os pontos A e E indicados no gráfico estão intercalados por um ciclo, o que signficia que o comprimento de m que separa estes pontos corresponde ao comprimento de onda. O enunciado disse pra gente que a velocidade de propagação da onda é de , dessa forma a gente pode calcular a frequência:
Passo 3
II e III estão corretas. Os pontos da corda oscilam em movimento harmônico simples (MHS) numa direção perpendicular à da propagação ondulatória. Nos pontos de inversão do sentido do movimento, o deslocamento é máximo (igual à amplitude das oscilações), a velocidade é nula e a aceleração tem máxima inteisdade , em que , e é a amplitude do MHS).
Observando no gráfico, note que no instante considerado, os pontos A, C e E têm velocidadenula, e por isso as alternativas I e II estão corretas.
Passo 4
IV está incorreta. Quem se desloca na velocidade de é a onda e não os pontos da corda.
Resposta
(C)