Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade e Potência de uma Onda na Corda

Ver Teoria
Exercício 4312345678910111213141516171819202122232425262728293031323334353637383940414244454647484950515253545556575859

Enunciado

Os itens são independentes. Indique a resposta com o número de algarismos significativos adequados.

a) Uma onda senoidal com período T = 2,00 m s se propaga em uma corda. Sabendo que, para dois pontos da corda separados por 0,117 m , a diferença de fase é de 60,0 ° , determine a velocidade da onda na corda.

b) A equação que descreve uma onda transversal em uma corda é y ( x , t ) = ( 2,00 m m ) s e n ( k x   -   600   r a d   s - 1 t ) . Sabendo que esta onda ao se refletir em um anteparo produz um padrão estacionário para o segundo harmônico em uma corda com comprimento L = ( π / 10,0 )   m , determine a velocidade da onda.

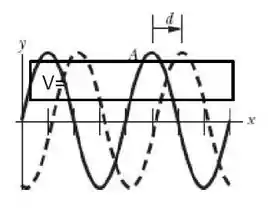
c) A figura mostra dois instantes t 1 (linha contínua) e t 2 (linha tracejada) de uma onda que se propaga em uma corda. Sabendo que a distância d é igual a 0,0250   m , que ∆ t = t 2 - t 1 = T / 4 e a frequência angular é π 20,0 × 10 3 r a d / s determine a velocidade da onda.

Passo 1

a) Como ele disse que é uma onda senoidal podemos escrever:

x t = x m sin ⁡ ω t + φ

Em que:

ω = 2 π T

E como ele deu o período:

ω = 2 π T = 2 π 2 × 10 - 3

ω = 1000 π

Então:

x t = x m sin ⁡ 1000 π t + φ

Show! Aí ele disse que a distância entre dois pontos é 0,117   m e que a diferença de fase entre eles é de 60 ° . Isso quer dizer que:

x 1 = x m sin ⁡ 1000 π t 1 + φ

x 2 = x m sin ⁡ 1000 π t 2 + φ

x 2 = x 1 + 0,117

E a diferença entre os argumentos dos senos vai ser 60 ° . Mas temos que usar em radianos! Então:

1000 π t 2 + φ - 1000 π t 1 + φ = π 3   r a d = 60 °  

1000 π t 2 - t 1 = π 3  

t 2 - t 1 ≅ 0,0003   s

Show, aí que vem o pulo do gato. Esse vai ser o tempo que a onda vai demorar pra percorrer 0,117   m . Então:

v = ∆ S ∆ t = 0,117 0,0003

v ≅ 390   m / s

Passo 2

B) Temos uma onda, com a seguinte característica

Onde n = 2 , o comprimento de onda L = π 10 = λ . Do enunciado ainda tiramos pela equação da onda que ω = 600   r a d / s . Logo a velocidade da onda é

v = ω k = 600 2 π π 10 = 30   m / s

Passo 3

c) Temos algumas informações importantes que já podemos tirar de cara do enunciado

ω = π 20 × 10 - 3 r a d s

Com essa informação, conseguimos descobrir o período da onda

T = 2 π ω = 2 π π 20 × 10 - 3 = 40   m s

Logo a velocidade será a distancia sobre o tempo, ou matematicamente

v = ∆ S ∆ t = 0,0250 40 4 × 10 - 3 = 2,5   m / s

Resposta

a) 3 90 m s

b) 30   m / s

c) 2,5   m / s

Exercícios de Livros Relacionados

A figura mostra o deslocamento y do ponto de uma corda situado em x = 0 em função do tempot quando uma onda passa pelo ponto. A escala do eixo y é definida por y=6,0m m . A onda tem a forma y x ,t = y
Em um experimento com ondas estacionárias, uma corda de 90c m de comprimento está presa a um dos braços de um diapasão excitado eletricamente, que oscila perpendicuJarmente à corda com uma frequência
Uma onda senoidal transversal se propaga em corda no sentido positivo de um eixo x com uma velocidade de 80m / s . No instante t = 0 , uma partícula da corda situada em x = 0 possui um deslocamento tr
Na figura a , a corda 1 tem uma massa específica linear de 3,00g / m e a corda 2 tem uma massa específica linear de 5,00g / m . As cordas estão submetidas à tensão produzida por um bloco suspenso de m
A figura mostra a velocidade transversal u em função do tempo t para o ponto de uma corda situado em x = 0 , quando uma onda passa por ele. A escala do eixo vertical é definida por u s = 4,0m / s . A